Perspective Projection

上篇筆記中有些東西我們還沒講，現在補充下哈。

在上一篇筆記中，我們在正交投影中提到了我們會把一個長方體變換為一個正立方體。而該長方體是由長寬高定義的，但是在此我們提出一個實際在使用的定義方式。

我們使用 field-of-view (fovY) 與 aspect ratio (寬 / 高) 定義。

考慮下圖情況，這是用側面去看該長方體。

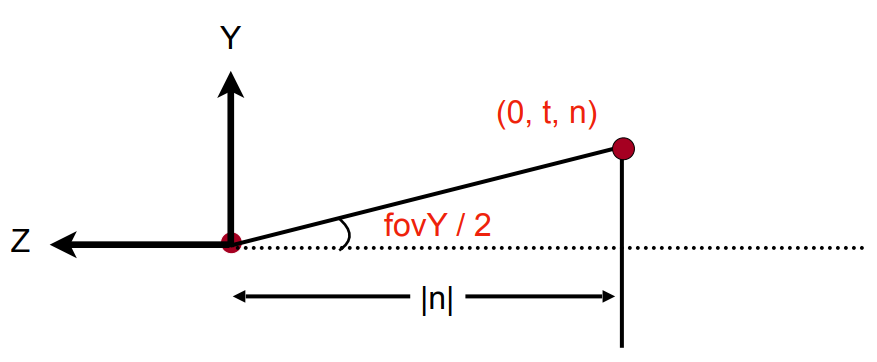
我們可以列出一些關係，可以幫助我們計算：

$\tan\left( \frac{\text{fovY}}{2} \right)=\frac{t}{|n|}\quad \text{aspect}=\frac{r}{t}$

What’s after MVP?

當我們做完 MVP 後，我們可以得到一個正立方體。然後呢？我們想要把它映射到螢幕上。

想要把東西映射到螢幕上，我們必須給螢幕定義一個螢幕空間。那麼我們就令原點處於螢幕的最左下角，$+x$ 向右，$+y$ 向上。

我們還定義一個像素的座標為該像素左下角的座標，而像素的正中心為該像素座標 $(x,y)$ 各自偏移 $0.5$。也就是說 $(x+0.5, y+0.5)$。

那麼，我們現在的任務就變成了將 $[1,1]^{2}$ 映射到 $[0,\text{width}]\times[0,\text{height}]$ 上。

注意到，這個變換與 $z$ 座標無關。我們可以得出此變換的矩陣：

$\begin{bmatrix} \frac{\text{width}}{2} & 0 & 0 & \frac{\text{width}}{2} \\ 0 & \frac{\text{height}}{2} & 0 & \frac{\text{height}}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

Sampling

現在我們已經得到了一個標準立方體，那我們應該如何知道螢幕上哪些點要顯示出圖像？我們使用採樣技術。

也就是說，假設我們要渲染一個三角形，那麼位於三角形內部的像素 (像素中心落在三角形內部的話) 應該要被上色。

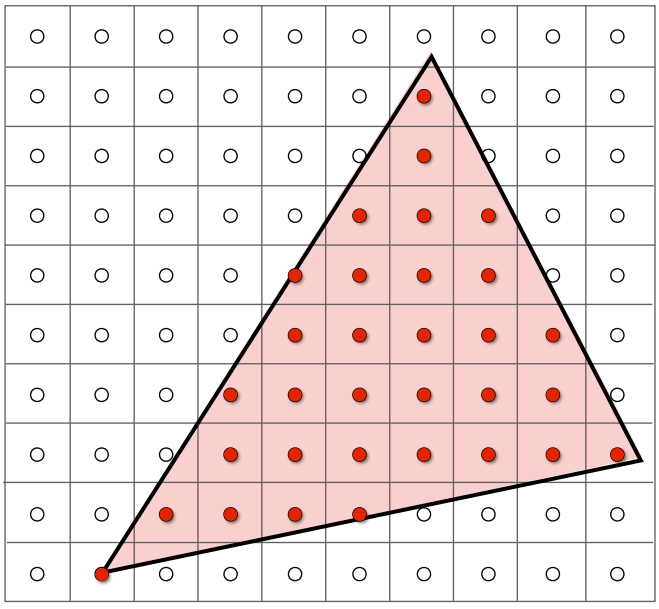
我們可以簡單用以下偽代碼展示這個過程：

1
2
3

for (int x = 0; x < xmax; x++)
	for (int y = 0; y < ymax; y++)
		image[x][y] = inside(tri, x + 0.5, y + 0.5)    // notice that we check whether the ceter of a pixel in the triangle or not

那我們應該和判斷一個點是否在三角形內部？

考慮下圖場景：

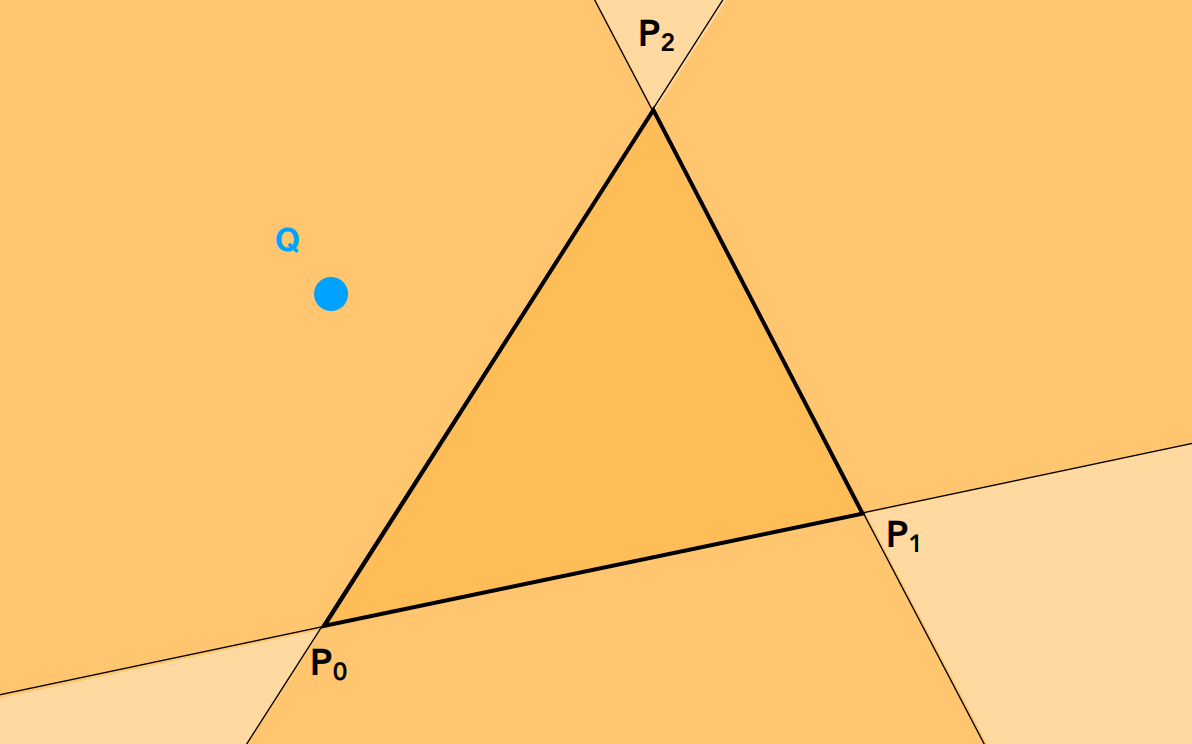
我們按照順時針或逆時針順序，連接頂點與 $Q$ 點 $P{i}Q$ ，並連接 $P{i}$ 按照順時針順序或逆時針順序的鄰居 $P{i}P{j}$。

按照順時針或逆時針方向依序計算所有 $P{i}Q\times P{i}P_{j}$。得出的結果如果全部同號，就代表 $Q$ 位於三頂點構成的三角形內，否則就在三角形外。

例如：

$P{0}Q\times P{0}P_{2}\implies -$

$P{2}Q\times P{2}P_{1}\implies+$

$P{1}Q\times P{1}P_{0}\implies+$

代表 $Q$ 在三角形外。

至於那些落在邊上的點，可以依你的喜好將其認為是落在三角形的內部或外部都可。

但其實，我們沒必要對螢幕上的所有像素都做如此檢查。

考慮下圖，明顯沒必要檢查最左邊那一 column 的像素。

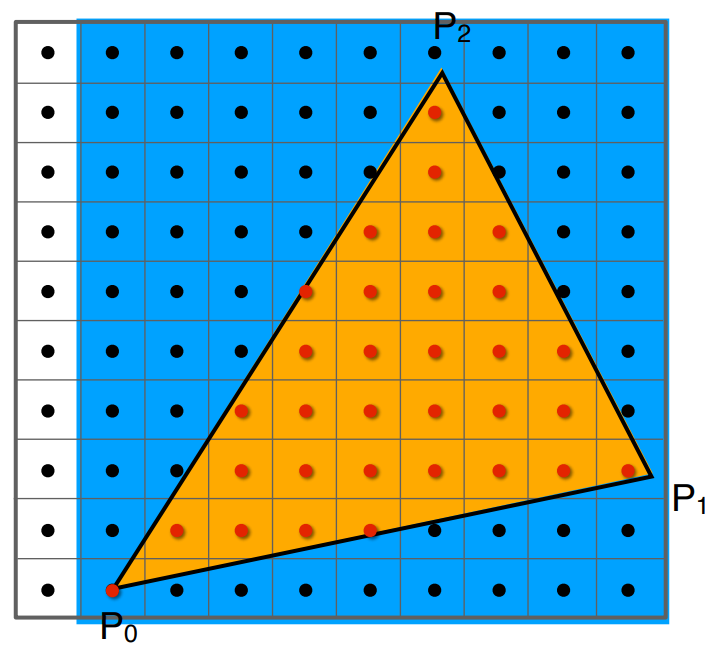
所以，我們實際要檢查的範圍其實是取 $x$ 的最大值與最小值、$y$ 的最大值與最小值。

這種技術我們稱為 Bounding Box。

考慮另一種極端情況，如果三角形極為細長，然後 $45^{\circ}$ 斜著放。這時雖然覆蓋面積較小，但是仍會造成 Bounding Box 較大的結果。

我們可以考慮另一種算法：

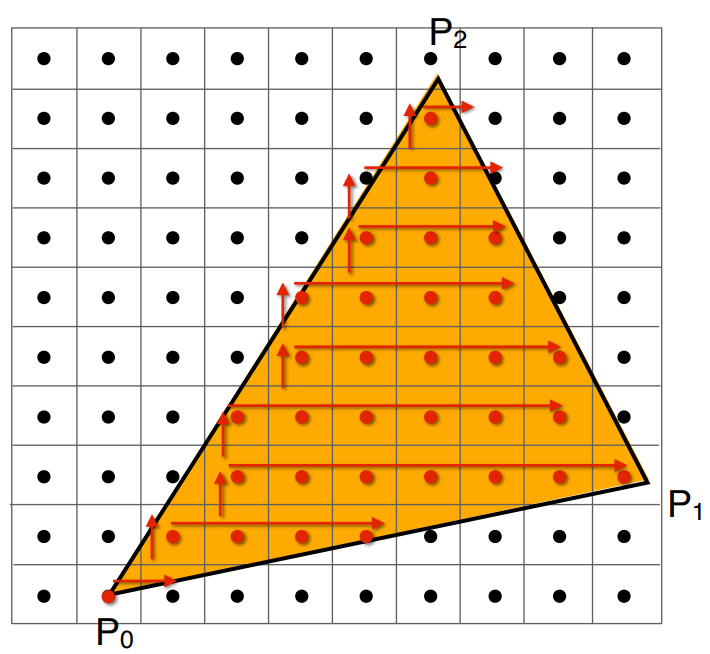
Aliasing

但由於我們採樣數可能不夠，會造成走樣問題。例如，我們用上述採樣方式得到的三角形如下：

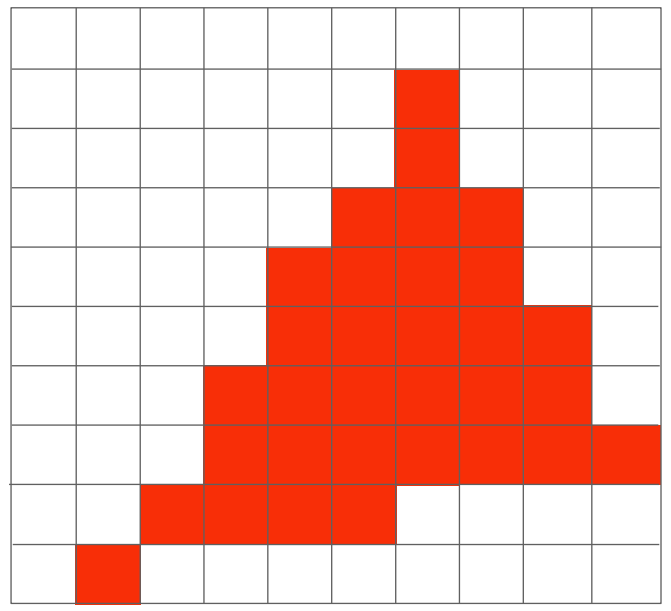
Antialiasing

如果想實現反走樣，可以考慮先將原三角形模糊後，再進行採樣。

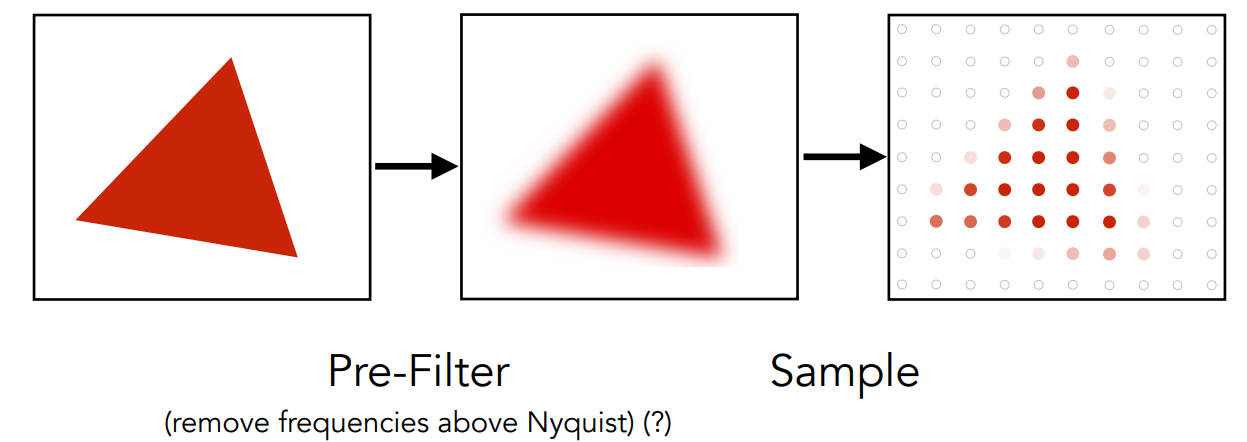
但是，如果我們先進行採樣，然後再模糊，取得的結果卻不是很好。

Frequency Domain

啥是頻域呀？就是一個波型的頻率分布圖。

我們可以通過傅立葉變換將一個函數 (空間域上) 轉換成頻率分布 (頻域上)。

而傅立葉變換的本質就是，通過函數的內積判斷與 $e^{i\omega x}$ 的遠近。

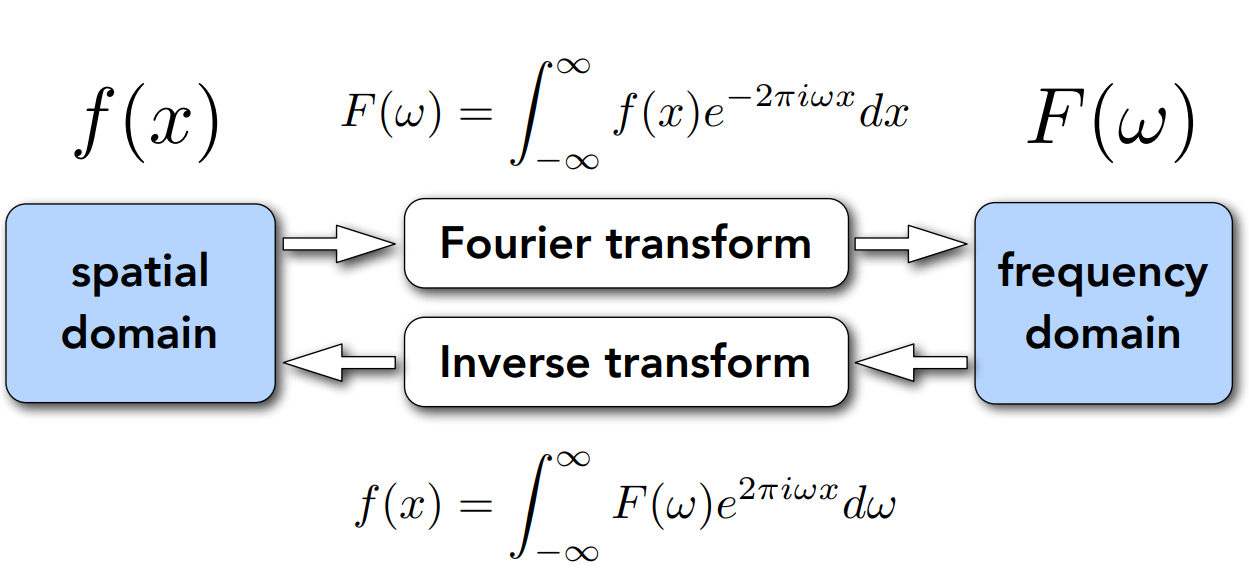
例如，將下左圖傅立葉變換後可以得到下右圖：

上右圖中心代表低頻，外圍代表高頻。而顏色越亮代表該頻率成分越多。

可以注意到，上左圖低頻成分較多。回憶低頻特性，震盪的較慢。反映在圖片中，就是較平滑處。

相反，如果是高頻的話，震盪的較快，反映在圖片中就是物體的邊緣，突然產生變化處。

所以，如果我們刪去低頻信號，然後使用逆傅立葉變換就會得到圖片的邊緣。我們稱這種過濾為：高通濾波。

相反，刪去高頻信號，會使得圖片變得模糊 (Blur) 。我們稱這種過濾為：低通濾波。

Convolution

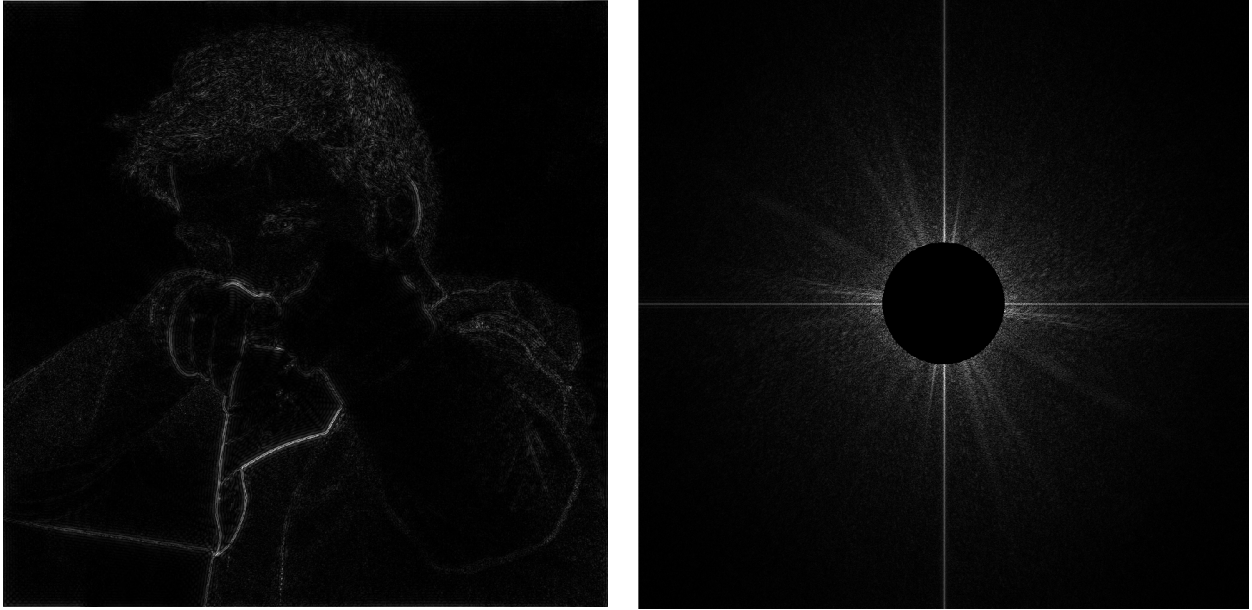
捲積是啥呀？就是給你一個捲積窗口，我們把對應的值做加權平均然後寫回。

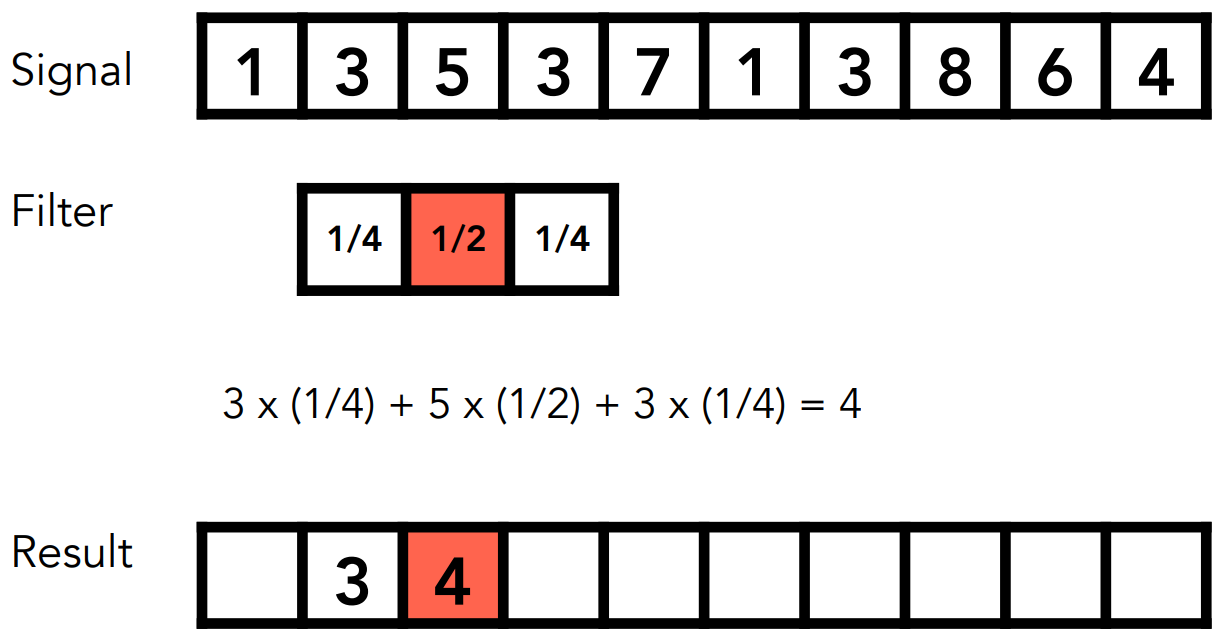
Convolution Theorem

簡單來說就是：

時域 (空間域) 的捲積 = 頻域的乘法
時域 (空間域) 的乘法 = 頻域的捲積

下圖左是 Box function 的函數圖形，二下圖右是 Box function 圖形經過傅立葉變換的樣子 (其實就是低通濾波) 。

如果將上圖右乘以某頻域上的圖，最後進行逆傅立葉變換，造成的效果與 Box filter 對原圖捲積造成的效果相同 (Blur) 。

Sampling = Repeating Frequency Contents

考慮 (a) 函數，我們用 (c) 對其採樣，得到 (e)。

如果轉換成頻域上的圖，會形如 (b) (d) (f)。

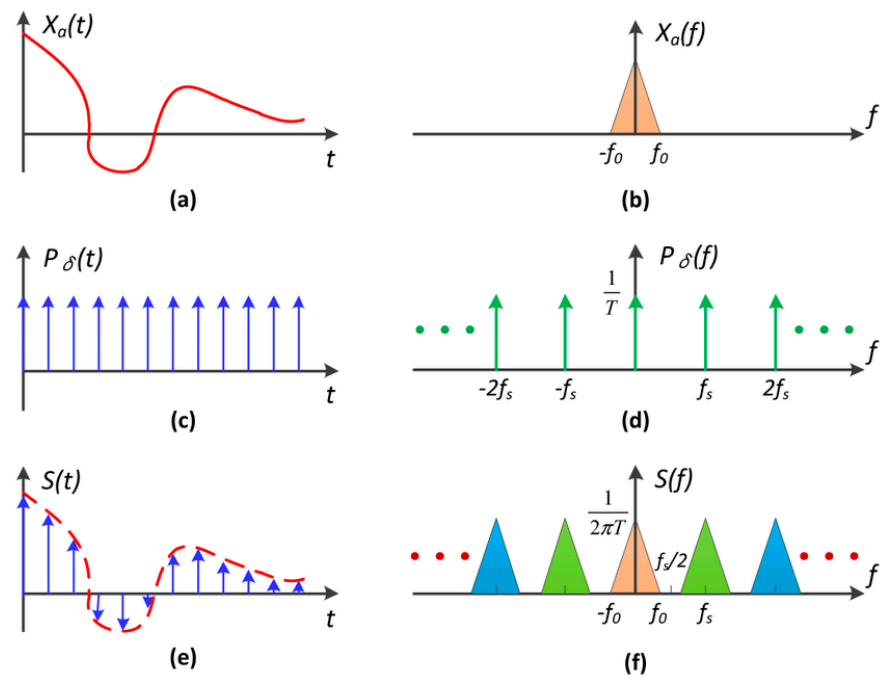
有了這個觀念，我們就可以解釋為啥之前說取樣數過少會造成走樣了。

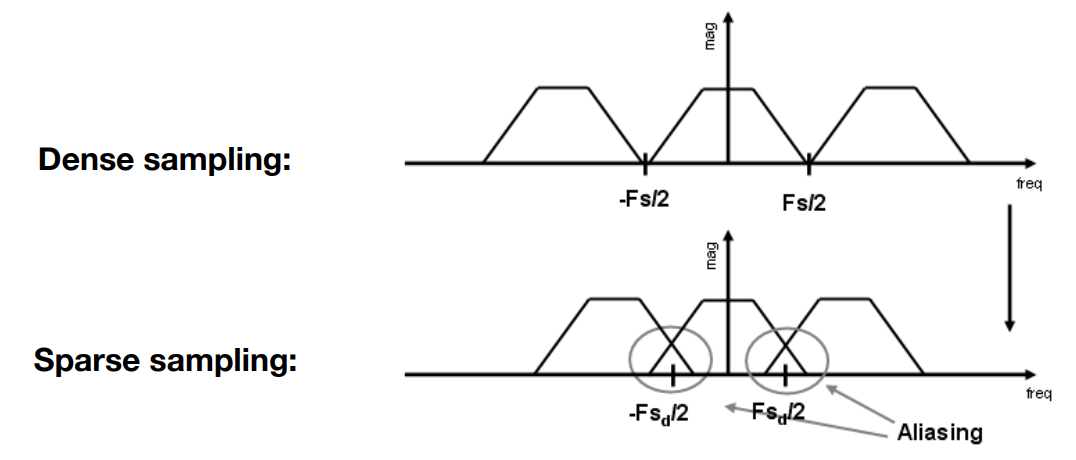
取樣數較少時，頻率較慢。會造成對應頻域上 ($x$ 軸是頻率) 間隔較少，使得圖像重疊而走樣。

Antialiasing

回憶開頭我們說如何做反走樣？先模糊後取樣。

也就是說，我們先套用一個低通濾波，過濾掉高頻信號 (使頻域上圖形變窄，因為高頻信號沒了) ，然後取樣。

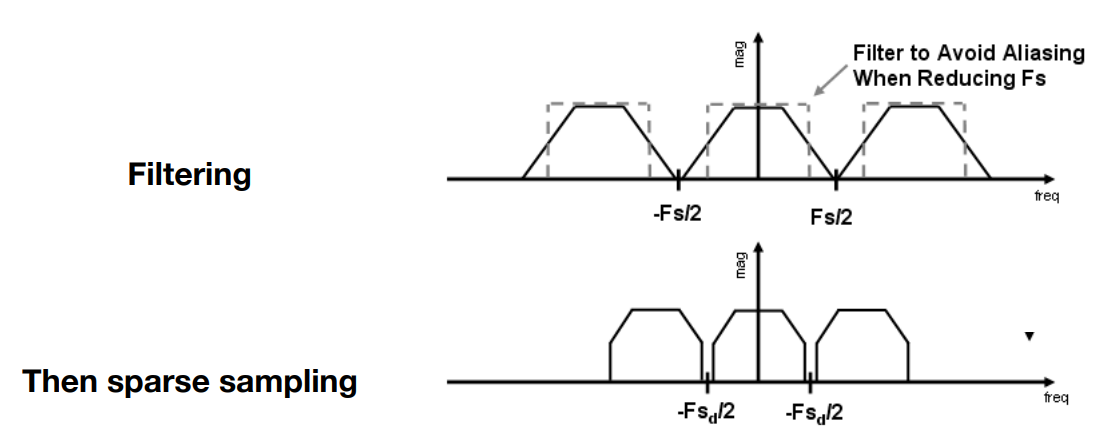
如上圖所示，可以有效減少圖形重疊問題。

所以，實際運用上我們可以如下操作：

對 $f(x,y)$ 用 1 像素的 box-blur 捲積。 (注意到捲積 = 濾波 = 平均)
對每個像素的中心取樣。

Antialiasing By Supersampling (MSAA, Multisampling Anti-Aliasing)

Supersampling 1

對每個像素再做 $n\times n$ 細分：

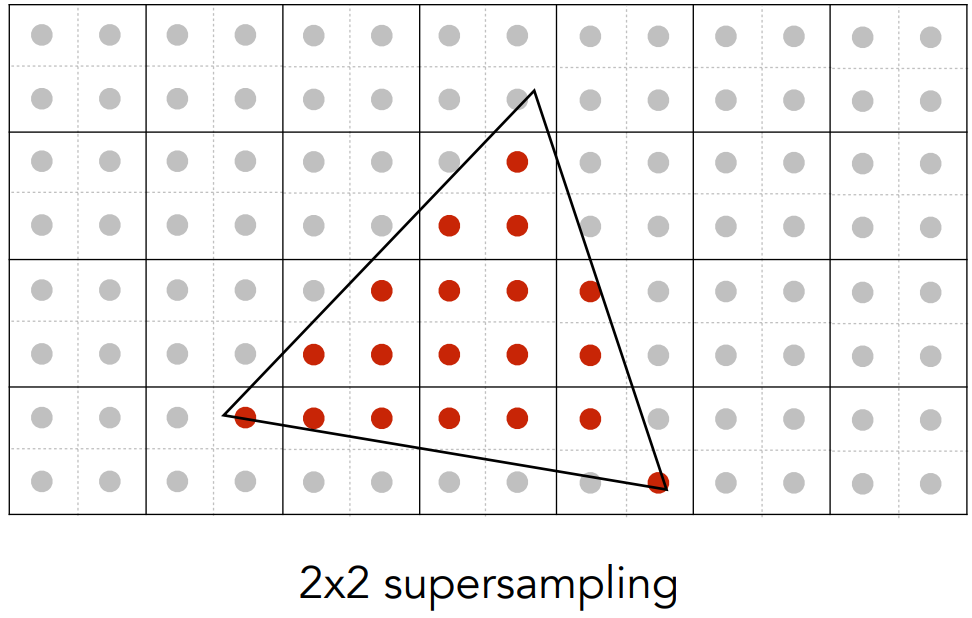
Supersampling 2

對每個像素中細分後落在三角形內部的數量做統計，數量越多顏色越深。

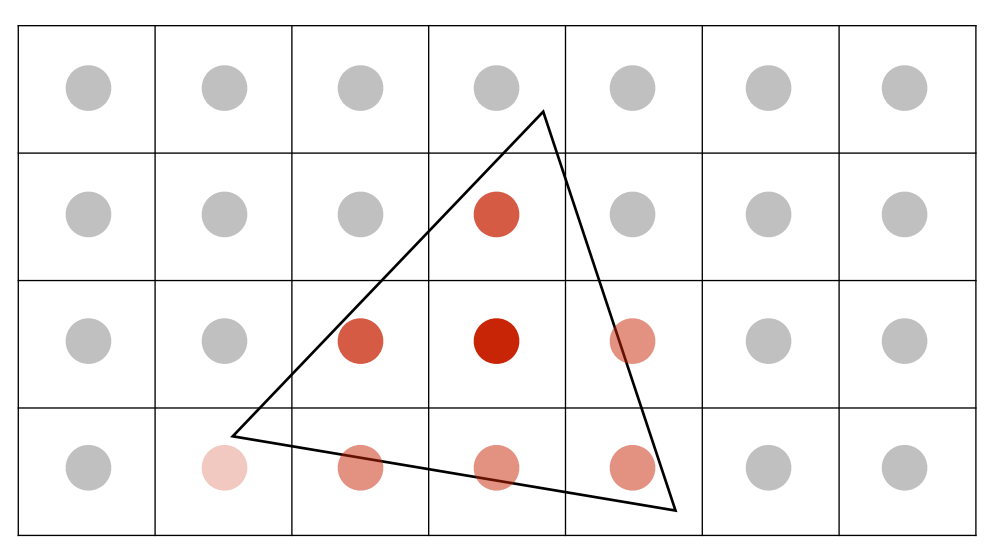
Visibility

在光栅化過程中，我們需要判斷物體的遮擋與可視關係。

最簡單的算法是畫家算法(Painter’s Algorithm)，從最深的物體開始繪製，並且不斷更新幀緩衝區。

畫家算法會有一個很大的問題，如果兩個三角形互相從中間穿過彼此，很可能沒法得出正確的渲染結果，因為我們無法判斷到底誰的深度較深。

Z-Buffer

最終解決此問題的方法是利用 Z 緩衝區。其核心思想是，存儲每個取樣點 (像素) 的深度信息。

所以，我們會需要兩個緩衝區。

幀緩衝區存儲顏色數據。
深度緩衝區存儲深度信息。

注意，為了方便理解，在此我們假設 $z$ 值越小，物體離攝像機越近。(與之前假設不同)

我們在此給出 Z-Buffer 算法的偽代碼：

注意初始化深度緩衝區為 $\infty$。

for (each triangle T)
	for (each sample (x, y, z) in T)
		if (z < zbuffer[x, y])
			framebuffer[x, y] = rgb; // update color
			zbuffer[x, y] = z;       // update depth
		else
			// do nothing, this sample is occluded

下圖展示了兩個互相穿過的三角形經過 Z 緩衝區算法正確顯示的過程：