為了使得位移運算可以通過矩陣乘法表達，我們使用齊次座標系統來表示三維座標中的點與向量。

也就是說：

$\text{point}=(x,y,z,1)^{T}\quad\text{vector}=(x,y,z,0)^{T}$

一般來說，若用 $(x,y,z,w)$ 表示一個點時 (其中 $w\neq 0$)，該點座標為： $\left( \frac{x}{w}, \frac{y}{w}, \frac{z}{w} \right)$。請記住這個結論，這對之後推導透視投影的矩陣很重要。

一個三維的縮放矩陣有如下形式：

$S(s_{x},s_{y},s_{z})=\begin{bmatrix} s_{x} & 0 & 0 & 0 \\ 0 & s_{y} & 0 & 0 \\ 0 & 0 & s_{z} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

位移矩陣：

$T(t_{x},t_{y},t_{z})=\begin{bmatrix} 1 & 0 & 0 & t_{x} \\ 0 & 1 & 0 & t_{y} \\ 0 & 0 & 1 & t_{z} \\ 0 & 0 & 0 & 1 \end{bmatrix}$

而三維的旋轉我們表達成對於 $x,y,z$ 三軸各自的旋轉：

$R_{x}(\alpha)=\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\alpha & -\sin\alpha & 0 \\ 0 & \sin\alpha & \cos\alpha & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \quad R_{y}(\alpha)=\begin{bmatrix} \cos\alpha & 0 & \sin\alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin\alpha & 0 & \cos\alpha & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \quad R_{z}(\alpha)=\begin{bmatrix} \cos\alpha & -\sin\alpha & 0 & 0 \\ \sin\alpha & \cos\alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

首先注意對於 $x,z$ 軸的旋轉矩陣，可以看出其實就是保持自己 ($x$ 或 $y$ 軸) 不變，然後對其他兩軸做二維旋轉。

比較特殊的是 $y$ 軸，可以看出它其實對其他二軸做了 $-\alpha$ 的二維旋轉。理由是這樣的，因為 $\mathbf{x}\times \mathbf{y}=\mathbf{z}$，且 $\mathbf{y}\times \mathbf{z}=\mathbf{x}$，但是 $\mathbf{x}\times \mathbf{z}=-\mathbf{y}$。這就是為甚麼旋轉 $-\alpha$ 的原因，我們要反著轉才能使得正確的旋轉到需要的角度。

如果我們看到形如：

$\begin{bmatrix} a & b & c & t_{x} \\ d & e & f & t_{y} \\ g & h & i & t_{z} \\ 0 & 0 & 0 & 1 \end{bmatrix}$

的變換矩陣，我們是先應用了線性變換還是位移？

這邊直接說答案，是先位移，然後應用線性變換。如果不相信可以自己驗證看看。

View / Camera Transformation

想將一堆三維座標或向量轉換到電腦螢幕上，需要經過以下三個矩陣的變換：

Model transformation：將模型從局部空間轉換到世界空間。
View transformation：將世界空間轉換到攝像機空間
Projection transformation：將攝像機空間中的視錐體映射到標準裁減空間。

我們現在聚焦在 View transformation

定義一個相機的位置，我們需要三個向量：

相機的座標向量。
相機的朝向 (Look-at) 向量。
相機的頭頂向量，因為攝像機可以左右傾斜，如果指定義朝向則無法辨別傾斜角度。

但是，想要讓攝像機在場景中自由移動，實現上並不是特別方便。事實上，我們令攝像機位置固定在原點 $(0,0,0)$ 並朝向 $-z$，頭頂向量指向 $y$。當攝像機移動時，其實是整個場景往攝像機的相反方向移動。

所以，想要構建一個這樣的矩陣，這個矩陣要有如下變換流程：

將物體移動到原點。
將物體朝向與 $-z$ 對齊。
將物體頭頂向量與 $y$ 對齊。
將物體朝向與頭頂向量的叉乘向量與 $x$ 對齊。

為了書寫方便，我們令物體位置為 $\vec{e}$，朝向 $\hat{g}$，頭頂向量 $\hat{t}$。並且 $M_{\text{view}}$ 為我們要求的變換矩陣。

總的來說，$M{\text{view}}$ 可以被寫成兩個矩陣相乘。一個 $T{\text{view}}$ 表示將物體移動到原點，一個 $R_{\text{view}}$ 將物體旋轉對齊到三根座標軸。

$T_{\text{view}}$ 很好求：

$T_{\text{view}}=\begin{bmatrix} 1 & 0 & 0 & -x_{e} \\ 0 & 1 & 0 & -y_{e} \\ 0 & 0 & 1 & -z_{e} \\ 0 & 0 & 0 & 1 \end{bmatrix}$

但是 $R{\text{view}}$ 不好求，考慮 $R{\text{view}}^{-1}$，也就是將三根座標軸旋轉到物體的對應三根向量上。我們可以較輕易的寫出這個矩陣：

$R_{\text{view}}^{-1}=\begin{bmatrix} x_{\hat{g}\times \hat{t}} & x_{t} & x_{-g} & 0 \\ y_{\hat{g}\times \hat{t}} & y_{t} & y_{-g} & 0 \\ z_{\hat{g}\times \hat{t}} & z_{t} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

我們通過修習線性代數，可以知道：一個單位矩陣的逆，就是該矩陣的轉置。

而一個旋轉矩陣因為有互相正交且長度為 $1$ 的 column vectors，所以旋轉矩陣是一個單位矩陣。

那麼我們有：$R{\text{view}}^{-1}=R{\text{view}}^{T}\implies R{\text{view}}=(R{\text{view}}^{-1})^{T}$。

所以：

$R_{\text{view}}=\begin{bmatrix} x_{\hat{g}\times \hat{t}} & y_{\hat{g}\times \hat{t}} & z_{\hat{g}\times \hat{t}} & 0 \\ x_{t} & y_{t} & z_{t} & 0 \\ x_{-g} & y_{-g} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

如此一來，就可以通過下式算得 $M_{\text{view}}$：

$M_{\text{view}}=R_{\text{view}}T_{\text{view}}$

Projection Transformation

Orthographic Transformation

這種投影方式比較容易實現，簡單來說就是將攝像機放到原點，看向 $-z$。然後將看到的所有東西的 $z$ 座標丟棄，並將所有東西縮放到 $[-1,1]^{2}$ 之間。

更一般的說，考慮下圖那樣的長方體。我們要將其放置到原點，然後縮放成邊長為 $2$ 的立方體。

需要注意到，因為面朝 $-z$，所以較近的面 $n$ 相對於較遠的面 $f$ 擁有更大的座標值。

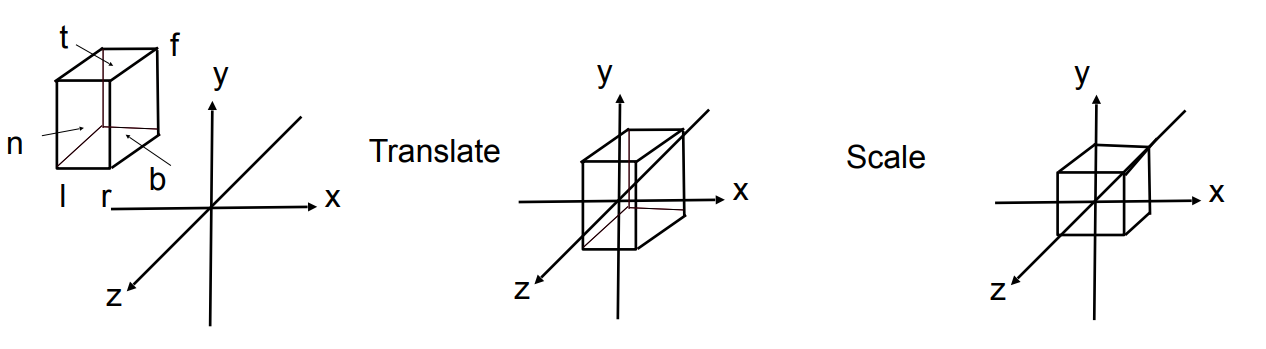
我們可以較輕易的將這個矩陣表達出來：

$M_{\text{ortho}}=\begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix}$

Perspective Transformation

如果想要直接將一個錐體較遠的一面映射到較近的一面，直接思考並不容易。

考慮下圖，如果我們將較遠的面向內擠壓 (較遠的面的 $z$ 軸座標值不變，但不保證兩面之間任意一點的 $z$ 值保持不變)，使得較近的面與較遠的面大小一致，我們就可以繼續套用上面求得的矩陣將其投影。

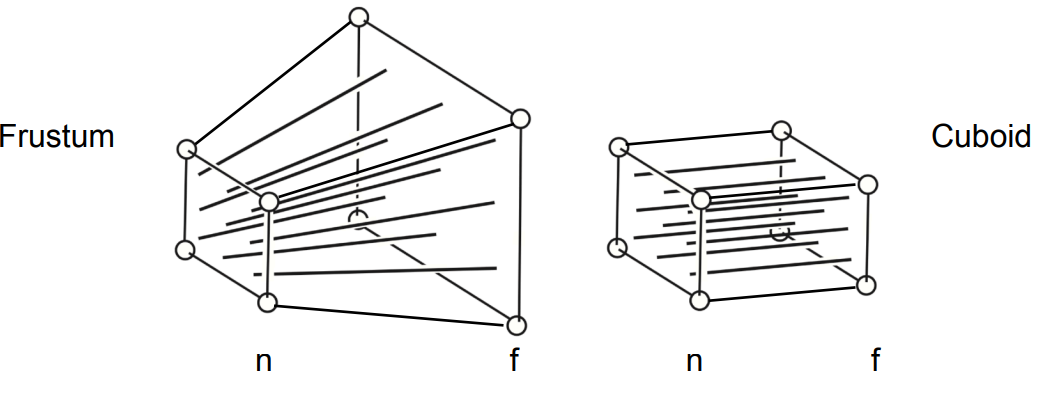
那我們應該如何知道要擠壓多少？考慮下圖，我們要使得 $y=y’$ 且 $x=x’$。

通過三角形相似，我們就可以得到結論 $y’=\frac{n}{z}y$ 且 $x’=\frac{n}{z}x$。

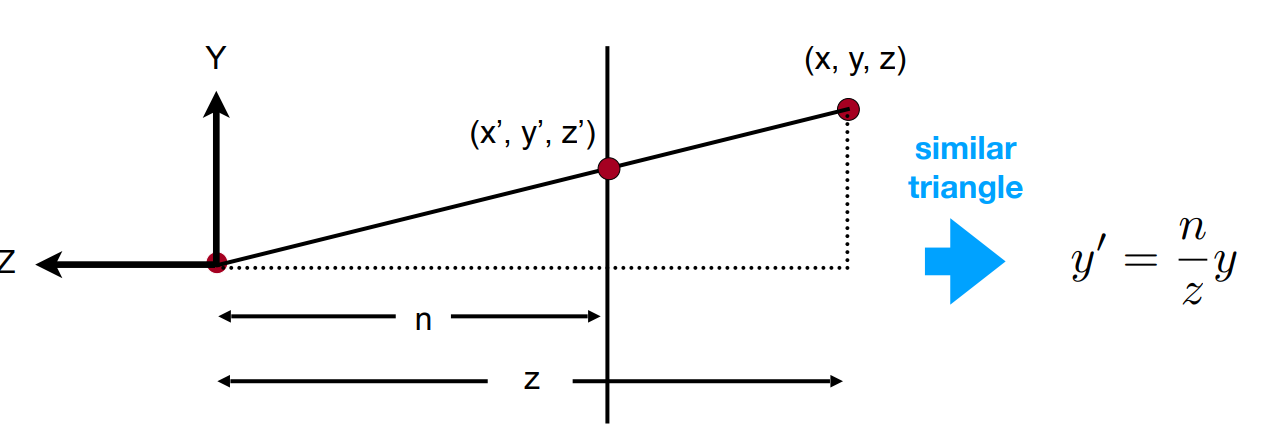
所以，在齊次座標上的任意點 $(x,y,z,1)^{T}$ 會被擠壓成 $\left( \frac{nx}{z}, \frac{ny}{z},\text{unknow},1 \right)$。

還記得用 $(x,y,z,w)$ 表示一個點時 (其中 $w\neq 0$)，該點座標為 $\left( \frac{x}{w}, \frac{y}{w}, \frac{z}{w} \right)$ 嗎？

所以，我們可以乘 $z$，得到的座標仍代表同一個點：$\left( \frac{nx}{z}, \frac{ny}{z},\text{unknow},1 \right)^{T}=(nx,ny,\text{unknow},z)^{T}$。

根據現有條件，我們有：

$M_{\text{persp}\to \text{ortho}}\begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} =\begin{bmatrix} nx \\ ny \\ \text{unknow} \\ z \end{bmatrix}\implies M_{\text{persp}\to\text{ortho}}=\begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \end{bmatrix}$

再根據：

近平面的 $z$ 不會因為擠壓而改變。
遠平面的 $z$ 不會因擠壓而改變。

我們有帶入條件，近平面的 $z$ 不會因為擠壓而改變：

$M_{\text{persp}\to \text{ortho}}\begin{bmatrix} x \\ y \\ n \\ 1 \end{bmatrix} =\begin{bmatrix} nx \\ ny \\ n^{2} \\ z \end{bmatrix}$

因為 $x$ 與 $y$ 與 $n$ 沒啥關係，所以 $\mathbf{e}_{3}^{T}M$ 就變為：

$\begin{bmatrix} 0 & 0 & A & B \end{bmatrix}$

將兩個條件帶入：

$\begin{align} & \begin{bmatrix} 0 & 0 & A & B \end{bmatrix}\begin{bmatrix} x \\ y \\ n \\ 1 \end{bmatrix}=n^{2} \\ & \begin{bmatrix} 0 & 0 & A & B \end{bmatrix}\begin{bmatrix} 0 \\ 0 \\ f \\ 1 \end{bmatrix}=f^{2} \end{align}$

就有：$A=n+f$ 與 $B=-nf$。

因為我們已經求得所有 $M_{\text{persp}\to\text{ortho}}$ 的元素，所以只需要套用下列公式就可以得到透視投影矩陣：

$M_{\text{persp}}=M_{\text{ortho}}M_{\text{persp}\to\text{ortho}}$