淺談內存分配器設計
前置知識
獨立內存空間
下圖展示了獨立內存空間的分佈。動態內存分配器(dynamic memory allocator) 就是一種在運行時堆(run-time heap) 上動態分配空間的工具。這裡我們特別注意一個變量brk,它指向堆的頂部。內存分配器就是通過增加它的值請求空間的。
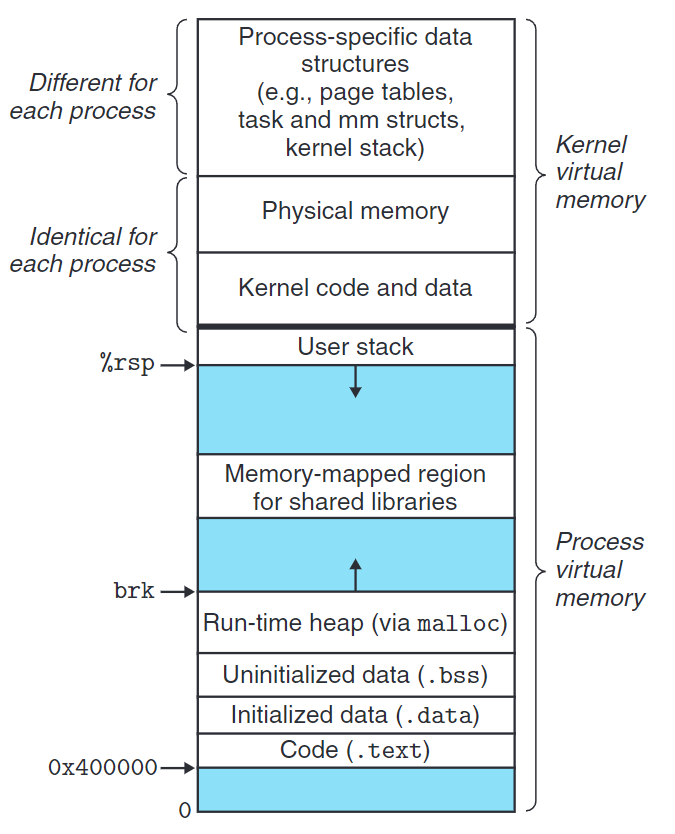
(引用書籍Computer Systems: A Programmer’s Perspective插圖,以下簡稱CSAPP)
內存分配
內存分配器分為兩種:
- 顯式分配器(explicit allocator):要求顯式地釋放已分配的塊。如
malloc, free或new delete。 - 隱式分配器(implicit allocator):或稱垃圾收集器(garbage collector),自動釋放已分配的塊(垃圾收集, garbage collection)。
本文主要介紹顯示分配器的實現。
當一塊區域的內存被分配後(指被如malloc之類的內存分配器分配),稱為已分配塊(allocated block)。
反之,還沒被分配的塊稱空閒塊(free block)。
碎片
碎片(fragmentation):指雖有未使用的內存,但不能滿足分配請求的現象。
有效載荷(payload):指分配器分配後,用戶實際可用的部分。(不包括 chunck header 和 pedding,這些名詞等下會解釋)
碎片分為兩種:
- 內部碎片:已分配塊比有效載荷大時發生。比如因內存對齊要求,使得分配塊比有效載荷大。內部碎片的大小,即已分配塊大小與有效載荷差的和。
- 外部碎片:當空閒內存合計起來足以滿足分配請求,但沒有單獨的空閒空間可以處理此請求時發生。比如,空閒塊與已分配塊交錯出現,而單個空閒塊又太小無法滿足要求。量化外部碎片比量化碎片難,因為它不只取決於先前請求模式和分配器實現方式,還取決於將來請求的模式。
內存分配器架構
想實現一個分配器,必須考慮以下問題:
- 空閒塊組織:如何記錄空閒塊?
- 放置:如何選擇合適的空閒塊來分配?
- 分割:當空閒塊被分配後,如何處理該空閒塊的剩餘部分?
- 合併:如何處理剛被釋放的塊?
我們可以使用一種稱空閒鏈表(free list) 的數據結構解決這些問題。
隱式空閒鏈表
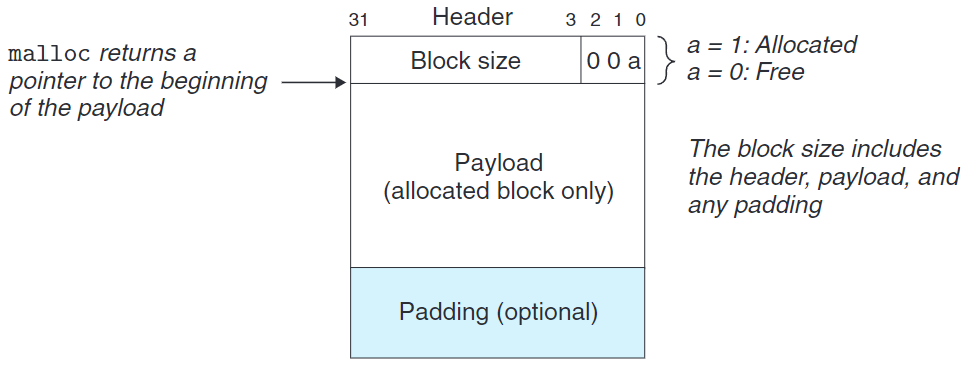
(引用書籍CSAPP插圖)
上圖展示了一個簡易的塊結構。
若我們強加一個(塊總大小)對8的對齊要求,則塊大小的最低3位必是0,所以存儲塊大小只需要29個高位。在這種情況下,低3位就可以拿來編碼其他信息(特別妙的一種想法)。此時,我們利用低3位標記此塊是否已分配。
例如,我們有一個已分配的塊,大小為24(0x18)字節。則他的頭部將是:
1 | 0x00000018 | 0x1 = 0x00000019 |
由上述的塊結構,我們可以將堆看做連續的已分配塊和空閒塊交錯出現的序列:

(引用書籍CSAPP插圖)
我們稱這種結構隱式空閒鏈表(implicit free list),因為空閒塊間由頭部的塊大小字段隱式連接著。在結構的最後,我們需要一種特殊標記的結束塊,此例中是一個設置已分配位且大小為零的終止頭部(terminating header)。
此結構的優點是簡單,缺點則是操作的開銷大。比如,要為新分配的塊選擇空閒塊放置。此時要對空閒鏈表進行搜索,且時間與堆中已分配塊和空閒塊總數呈線性關係。
注意,系統對齊要求和分配器塊數據結構格式會限制最小塊大小,沒有任何已分配塊可以比這個最小值小。例如,上述的塊格式導致最小的塊佔8字節。4字節作為 header,4字節用來維持對齊。
放置已分配塊
當應用請求塊,分配器搜索空閒鏈表,查找足夠放置所求塊的空閒塊。分配器執行搜索的方式由放置策略(placement policy) 確定。
以下是常見的策略:
- 首次匹配:從頭開始搜索,選擇第一個適合的空閒塊。
- 優點:傾向於將大空閒塊留在鏈表後面。
- 缺點:前面留下太多小空閒塊碎片,導致搜索較大塊的時間增加。
- 下一次匹配:從上一次查詢結束的地方開始搜索,選擇第一個適合的塊。
- 最佳匹配:檢查每個空閒塊,找到最適合的。
分割空閒塊
一旦找到合適的空閒塊,就必須做出另一個策略決定,分配這個塊中多少空間。
- 若匹配佳,選擇使用整個空閒塊。缺點:造成內部碎片。
- 若匹配不佳,分割空閒塊。
合併空閒塊
當分配器釋放已分配塊時,可能有其他空閒塊與新釋放的空閒塊相鄰。相鄰的空閒塊可能導致假碎片(fault fragmentation)。
為了解決此問題,分配器必須合併相鄰的空閒塊,此過程稱合併(coalescing)。合併分為立即合併與推遲合併(deferred coalescing),延遲合併會等某個分配請求失敗,才會掃描整個堆進行合併。
帶邊界標記的合併
假設我們稱想要釋放的塊為當前塊。想要合併處於當前塊的下一個空閒塊很簡單,只要檢查下一塊的頭部,並將它的大小加到當前塊的頭部即可。
但是若想合併處於當前塊之前的空閒塊,則必須整個重新遍歷一次鏈表。釋放的時間與堆的大小成線性關係。
Knuth提出邊界標記(boundary tag) 的技術,允許常數時間的合併。邊界標記通過往每個塊的結尾添加一個腳部(footer,亦稱邊界標記) 實現,腳部存放的是頭部的副本。當前塊可以通過訪問腳部來判斷當前塊之前的塊是否空閒。
對每個塊添加腳部貌似有點奢侈,其實,只有未分配塊才需要腳部。已分配塊只需要將已分配/空閒位存儲在當前塊的頭部低位(當前塊腳部仍保持當前塊的已分配/空閒位),就可以被當前塊識別,從而略過合併。但是,空閒塊仍需要腳部,因為當前塊需要從腳部取得塊大小。
顯式空閒鏈表
由於隱式空閒鏈表的塊分配與塊數量呈線性關係,所以不適合用於通用分配器。這時,顯式空閒鏈表(explicit free list) 較適用。
因為空閒塊不存儲用戶數據,我們可以將指針數據放在此處。例如,組織成一個雙向鏈表。這樣可以使分配時間從總塊數的線性時間減少到總空閒塊數的線性時間。
將釋放塊插入空閒鏈表有兩種策略:
- 後進先出(LIFO):將新釋放的塊放在鏈表頭部。複雜度:$O(1)$。
- 按地址順序:將新釋放的塊放在按地址大小排序的相應位置,因為必須遍歷找到新釋放塊的
pred和succ,所以複雜度較高。複雜度:$O(n)$。
按地址排序的首次適配有較高內存利用率,這也是為何就算時間複雜度較高也有人選用的原因。
顯式鏈表的缺點是,最小塊大小增加,提高內部碎片的程度。
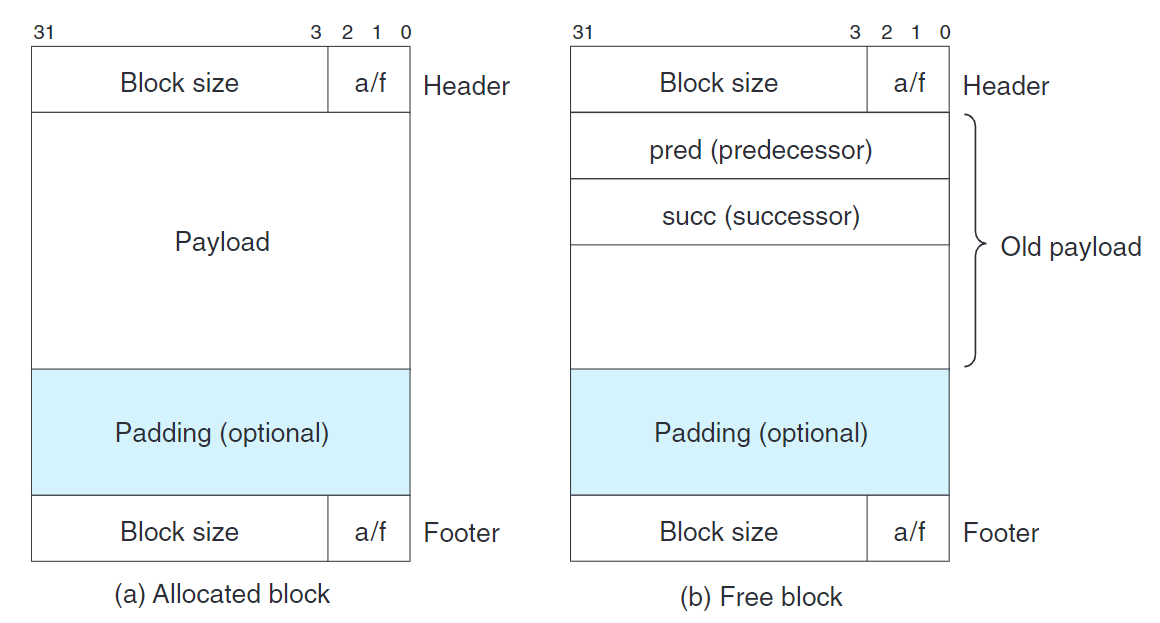
(引用書籍CSAPP插圖)
分離的空閒鏈表
分離的空閒鏈表(segregated free list) 的核心想法是,把不同大小的塊分開管理,每種大小一條鏈表。我們稱這些大小為等價類或大小類(size class)。
- 簡單的分離存儲
每個大小類的空閒鏈表都是大小相等的塊,每個塊的大小都是該大小類中最大元素的值。比如大小類定義為${ 17\sim 32 }$則每個塊大小都為32。 - 分離適配
對於不同大小類,分配器維護很多鏈表與之關聯。鏈表中,每個塊的大小都在相應大小類區間中。所以想要操作塊時,只要簡單的向對應鏈表搜索即可。
內存分配器實現
這裡我們選用CSAPP提供的 malloc lab 來實現一個簡化的內存分配器。
可以從這裡下載 malloc lab 的壓縮文件,從這裡取得官方操作說明。
閱讀以下內容前,請確保你已經下載並閱讀過官方操作說明。
選用架構
空閒鏈表:segregated free list。
大小類:共32條空閒鏈表,以2的冪做劃分,剛好可以覆蓋unsigned int的範圍。
未分配塊搜尋策略:最佳匹配。
空閒鏈表插入策略:LIFO。
常用宏實現
我定義了一些宏,專門用來執行指針運算。以免後續代碼中全是這種噁心的指針運算。
1 | /* basic constants */ |
函數定義
mm_init():這個函數實現分配器的初始化。
mm_malloc():實現類似malloc功能。
mm_free():實現類似free功能。
mm_realloc():實現類似realloc功能(因為這個函數是我最後寫的,前面debug找的非常煩躁,寫的比較醜陋請見諒)。
find_class():傳入空閒塊指針,返回對應大小類。
insert_list():將空閒塊插入到對應空閒鏈表中。
remove_list():將空閒塊從空閒鏈表中刪除(表示馬上要被分配了)。
coalesce():檢查當前塊的前一塊與後一塊,若也是空閒塊則合併。
extend_heap():設置brk,使堆增長。
find_fit():在鏈表中尋找合適大小的空閒塊。
place():修改空閒塊數據,使其成為已分配塊,並依大小決定是否分割。
代碼實現
代碼有一點點長,億點點醜陋,億點點臃腫…
所以我把它放在了github上面,需要可以取用(包含CSAPP其他lab的實現):https://github.com/ilsao/CSAPP-lab-solutions/blob/main/malloc%20lab/mm.c







![[GAMES 101] Rasterization 筆記](/pictures/SAO.jpg)


