前言 此實驗分為兩部分,Part A要求我們實現一個高速緩存模擬器,模擬高速緩存的行為。Part B要求優化一段轉置矩陣函數。
Part B 的優化使用分塊矩陣計算,涉及到線性代數的內容。我還沒有學習過,所以幾乎耗費兩小時時間在理解分塊矩陣乘法計算順序上面,推薦讀者可以先去了解相關資料再嘗試Part B。
Part A 此部分我們需要編寫一個高速緩存模擬器,讀取trace file,並模擬其讀取內存的行為。
1 2 3 4 I 0400 d7d4,8 M 0421 c7f0,4 L 04f 6b868,8 S 7f f0005c8,8
以上是一個trace file內容的例子。其中I表示指令加載,我們的模擬器不用模擬這種加載。L表示數據加載,S表示數據儲存,M表示數據修改(我們以一次數據加載後跟著一個數據儲存來模擬這種行為)。
以下是我們想要達成的目標:
1 Usage: ./csim [-hv] -s <s> -E <E> -b <b> -t <tracefile>
• -h: Optional help flag that prints usage info-v: Optional verbose flag that displays trace info-s <s>: Number of set index bits (S = $2^{s}$ is the number of sets)-E <E>: Associativity (number of lines per set)-b <b>: Number of block bits (B = $2^{b}$is the block size)-t <tracefile>: Name of the valgrind trace to replay
對於以上輸入,輸出對應的命中、不命中和驅逐數。
1 2 linux> ./csim -s 4 -E 1 -b 4 -t traces/yi.trace hits:4 misses:5 evictions:3
命令行參數解析 我使用頭文件getopt.h來幫助解析命令行參數。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 if (argc == 2 && argv[1 ][1 ] == 'h' ) { ShowHelp(); return 0 ; } if (argc != 10 && argc != 9 ) { printf ("./csim: Missing required command line argument\n" ); ShowHelp(); return -1 ; } while ( (opt = getopt(argc, argv, "hvs:E:b:t:" )) != -1 ) { switch (opt) { case 'h' : ShowHelp(); return 0 ; case 'v' : v = true ; break ; case 's' : s = atoi(optarg); break ; case 'E' : E = atoi(optarg); break ; case 'b' : b = atoi(optarg); break ; case 't' : tracefile = malloc (sizeof (strlen (optarg+1 ))); tracefile = optarg; break ; default : break ; } }
這部分不涉及困難知識,僅放代碼以供參考。
結構定義 回想高速緩存的結構:有$S$個組,每個組中有$E$個高速緩存行。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 typedef struct _cacheLine { bool valid; unsigned int tag; char *bytes; unsigned int callTime; }cacheLine; typedef struct _cacheSet { cacheLine *line; }cacheSet; typedef struct _dataCache { unsigned int s; unsigned int E; unsigned int b; cacheSet *set ; }dataCache;
我使用dataCache結構代表整個高速緩存,因為$S$、$E$的大小是可變的,所以需要使用malloc為其分配空間,故dataCache的set應為指針,同理line也是。
其中,cacheLine下的callTime用來記錄最後一次該行被使用的時間,用來實現Least-Recently Used驅逐策略。
初始化高速緩存 因為命令行參數輸入的值是$(s, E, b)$,而組的數量為$2^{s}$,所以我們需要通過左移計算出組的數量。$1$左移$n$位就代表$2^{n}$。
1 2 3 4 5 6 7 8 9 10 11 12 13 unsigned int S = 1 << s; dataCache cache; cache.s = s; cache.E = E; cache.b = b; cache.set = malloc (sizeof (cacheSet) * S); for (int i = 0 ; i < S; i++) { cache.set [i].line = malloc (sizeof (cacheLine) * E); cache.set [i].line->valid = false ; cache.set [i].line->tag = -1 ; cache.set [i].line->callTime = 0 ; }
初始化高速緩存需要將有效位(valid)設為false,因為我們需要模擬冷啟動。而tag設置為-1而不是0則是為了避免某些地址計算出來的tag等於0的問題。
主模擬函數 我們將tracefile中的每一行分為三個部分op、addr和bytes。op是操作符,代表其執行L、S和M中的一個。addr是操作的地址,而bytes是需要操作多少字節。
其實實驗文檔中有提到,我們可以假設所有的內存訪問都是對齊的,也就是說可以忽略跨塊訪問的問題。那我們其實可以很簡單的將bytes忽略而不用模擬。
為了計算某地址會被映射到高速緩存的哪個位置,我們需要將地址劃分為三個部分,分別是tag、set和byte。
我們發現:對於L、S和M操作,可以簡單的將其視為類似的操作,只是M需要操作兩次。因為我們的目標是模擬,而不是確實實現高速緩存(我們不往塊裡面寫數據)。所以我簡單的將L操作下的代碼複製給了S和M,這些代碼本來應該被封裝成一個函數,但是既然我已經完成了實驗,就沒有對其繼續優化。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 bool Simulate (char *tracefile, dataCache *cache, bool v, int *hit_count, int *miss_count, int *evict_count) { FILE *file = fopen(tracefile, "r" ); char buf[BUF_SIZE]; char *op, *addr, *bytes; if (file == NULL ) { printf ("%s: No such file or directory.\n" , tracefile); return false ; } unsigned int timer = 0 ; while (fgets(buf, BUF_SIZE, file) != NULL ) { if (buf[0 ] == 'I' ) continue ;; timer++; op = strtok(buf, " " ); addr = strtok(NULL , "," ); bytes = strtok(NULL , " \n" ); unsigned int set , tag, line; set = FindSet(cache, addr); tag = FindTag(cache, addr); switch (*op) { case 'L' : if ( (line = FindLine(cache, set , tag, timer)) != -1 ) { *hit_count += 1 ; if (v) { ShowDetail(op, addr, bytes, "hit " ); } } else { *miss_count += 1 ; if (!IsSetFull(cache, set )) { StoreCache(cache, set , tag, timer); if (v) { ShowDetail(op, addr, bytes, "miss " ); } } else { *evict_count += 1 ; EvictLine(cache, set ); StoreCache(cache, set , tag, timer); if (v) { ShowDetail(op, addr, bytes, "miss eviction " ); } } } if (v) printf ("\n" ); break ; case 'S' : if ( (line = FindLine(cache, set , tag, timer)) != -1 ) { *hit_count += 1 ; if (v) { ShowDetail(op, addr, bytes, "hit " ); } } else { *miss_count += 1 ; if (!IsSetFull(cache, set )) { StoreCache(cache, set , tag, timer); if (v) { ShowDetail(op, addr, bytes, "miss " ); } } else { *evict_count += 1 ; EvictLine(cache, set ); StoreCache(cache, set , tag, timer); if (v) { ShowDetail(op, addr, bytes, "miss eviction " ); } } } if (v) printf ("\n" ); break ; case 'M' : if ( (line = FindLine(cache, set , tag, timer)) != -1 ) { *hit_count += 1 ; if (v) { ShowDetail(op, addr, bytes, "hit " ); } } else { *miss_count += 1 ; if (!IsSetFull(cache, set )) { StoreCache(cache, set , tag, timer); if (v) { ShowDetail(op, addr, bytes, "miss " ); } } else { *evict_count += 1 ; EvictLine(cache, set ); StoreCache(cache, set , tag, timer); if (v) { ShowDetail(op, addr, bytes, "miss eviction " ); } } } if ( (line = FindLine(cache, set , tag, timer)) != -1 ) { *hit_count += 1 ; if (v) { printf ("hit " ); } } else { *miss_count += 1 ; if (!IsSetFull(cache, set )) { StoreCache(cache, set , tag, timer); if (v) { printf ("miss " ); } } else { *evict_count += 1 ; EvictLine(cache, set ); StoreCache(cache, set , tag, timer); if (v) { printf ("miss eviction " ); } } } if (v) printf ("\n" ); break ; default : break ; } } fclose(file); return true ; }
在這個Simulate()函數裡面,可以發現許多還沒講解的函數。
unsigned int FindTag(dataCache *cache, char *addr):給定cache和addr,尋找對應的標籤。
unsigned int FindSet(dataCache *cache, char *addr):給定cache和addr,尋找對應的組。
unsigned int FindLine(dataCache *cache, unsigned int set, unsigned int tag, unsigned int timer):尋找某個高速緩存行,等同於對其訪問,所以會更新其callTime。
bool IsSetFull(dataCache *cache, unsigned int set):確定某個組是否已滿。
void StoreCache(dataCache *cache, unsigned int set, unsigned int tag, unsigned int timer):將內存數據寫到高速緩存中。
void EvictLine(dataCache *cache, unsigned int set):利用LRU規則,驅逐組中的某一行。
核心函數實現 FindTag()1 2 3 4 5 6 7 8 9 unsigned int FindTag (dataCache *cache, char *addr) { unsigned int d_addr = strtol(addr, NULL , 16 ); unsigned int tag = d_addr >> ((cache->s) + (cache->b)); return tag; }
首先我們將addr從char*轉換成十進制的unsigned int。
還記得我們將addr劃分為三個部分,分別是tag、set和byte,現在我們要取得tag。
想要取得tag,我們需要回想書中第二章的內容。將整個d_addr右移s+b位即可。
FindSet()1 2 3 4 5 6 7 8 9 10 unsigned int FindSet (dataCache *cache, char *addr) { unsigned int d_addr = strtol(addr, NULL , 16 ); unsigned int mask = (1 << ((cache->s) + (cache->b))) - 1 ; unsigned int set = (d_addr & mask) >> (cache->b); return set ; }
想要取得set,我們使用遮罩將tag部分的數據過濾,然後再右移b位即可。
生成遮罩我們只要通過將1左移到第s+b位的左邊一位,然後剪掉1,就可以生成從第一位到第s+b位都是1的遮罩。
然後將d_addr與遮罩做與運算,就可以過濾掉tag。
FindLine()1 2 3 4 5 6 7 8 9 10 unsigned int FindLine (dataCache *cache, unsigned int set , unsigned int tag, unsigned int timer) { unsigned int line = -1 ; for (int i = 0 ; i < cache->E; i++) { if (cache->set [set ].line[i].tag == tag && cache->set [set ].line[i].valid) { line = i; cache->set [set ].line[i].callTime = timer; } } return line; }
我們遍歷給定的某個set,當某一行的tag與我們給定的tag匹配,且該行有效的情況下,我們就找到了目標行。
同時,因為我們將尋找行當做訪問,所以需要更新該行的callTime。
IsSetFull()1 2 3 4 5 6 7 8 bool IsSetFull (dataCache *cache, unsigned int set ) { bool flag = true ; for (int i = 0 ; i < cache->E; i++) { if (!cache->set [set ].line[i].valid) flag = false ; } return flag; }
如果組內有任何一行的有效位無效,則返回false,否則返回true。
StoreCache()1 2 3 4 5 6 7 8 9 10 11 12 void StoreCache (dataCache *cache, unsigned int set , unsigned int tag, unsigned int timer) { for (int i = 0 ; i < cache->E; i++) { if (cache->set [set ].line[i].valid == false ) { cache->set [set ].line[i].valid = true ; cache->set [set ].line[i].tag = tag; cache->set [set ].line[i].callTime = timer; break ; } } }
我們可以省去檢查組是否已滿,因為Simulate函數已經幫我們檢查過了。
我們只需要找到空的行(有效位無效),然後將該行的有效位設置為有效,然後設置tag和callTime即可。
EvictLine()1 2 3 4 5 6 7 8 void EvictLine (dataCache *cache, unsigned int set ) { unsigned int minIndex = 0 ; for (int i = 0 ; i < cache->E; i++) minIndex = cache->set [set ].line[i].callTime < cache->set [set ].line[minIndex].callTime ? i : minIndex; cache->set [set ].line[minIndex].valid = false ; }
我們使用LRU策略來驅逐行,LRU策略就是驅逐距離上次被訪問時間最長的那一行。
通過遍歷每一行的callTime,我們對比minIndex和該行誰的callTime更小,較小的那行成為新的minIndex值。
最後,當遍歷完整個組,驅逐第minIndex行。
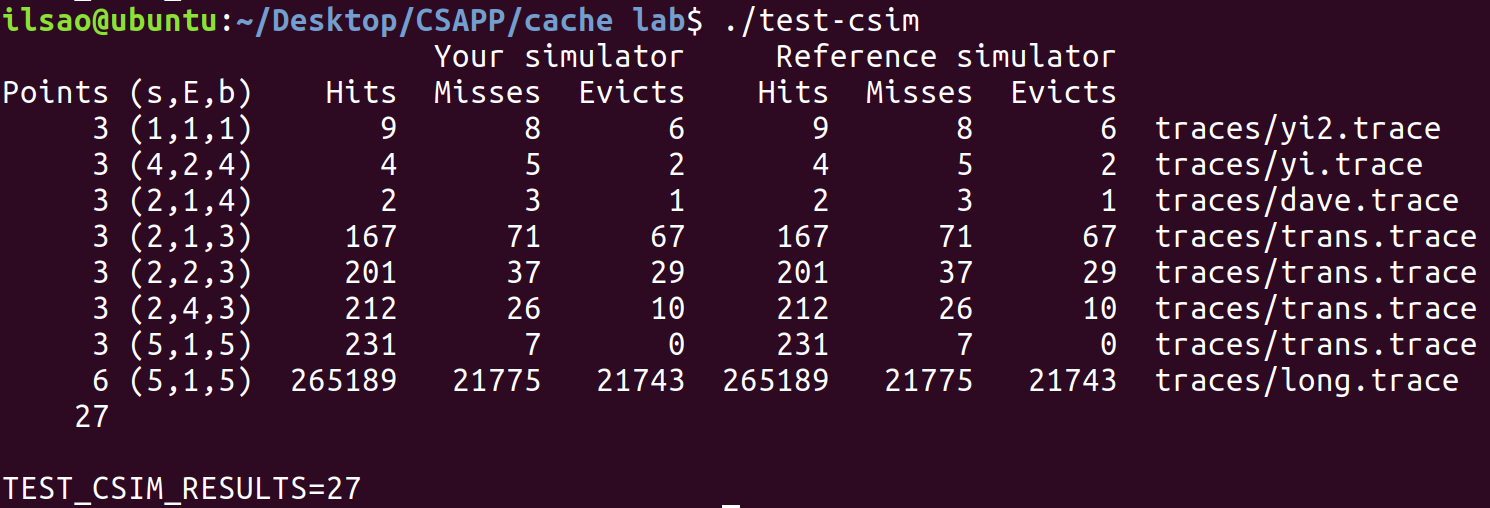
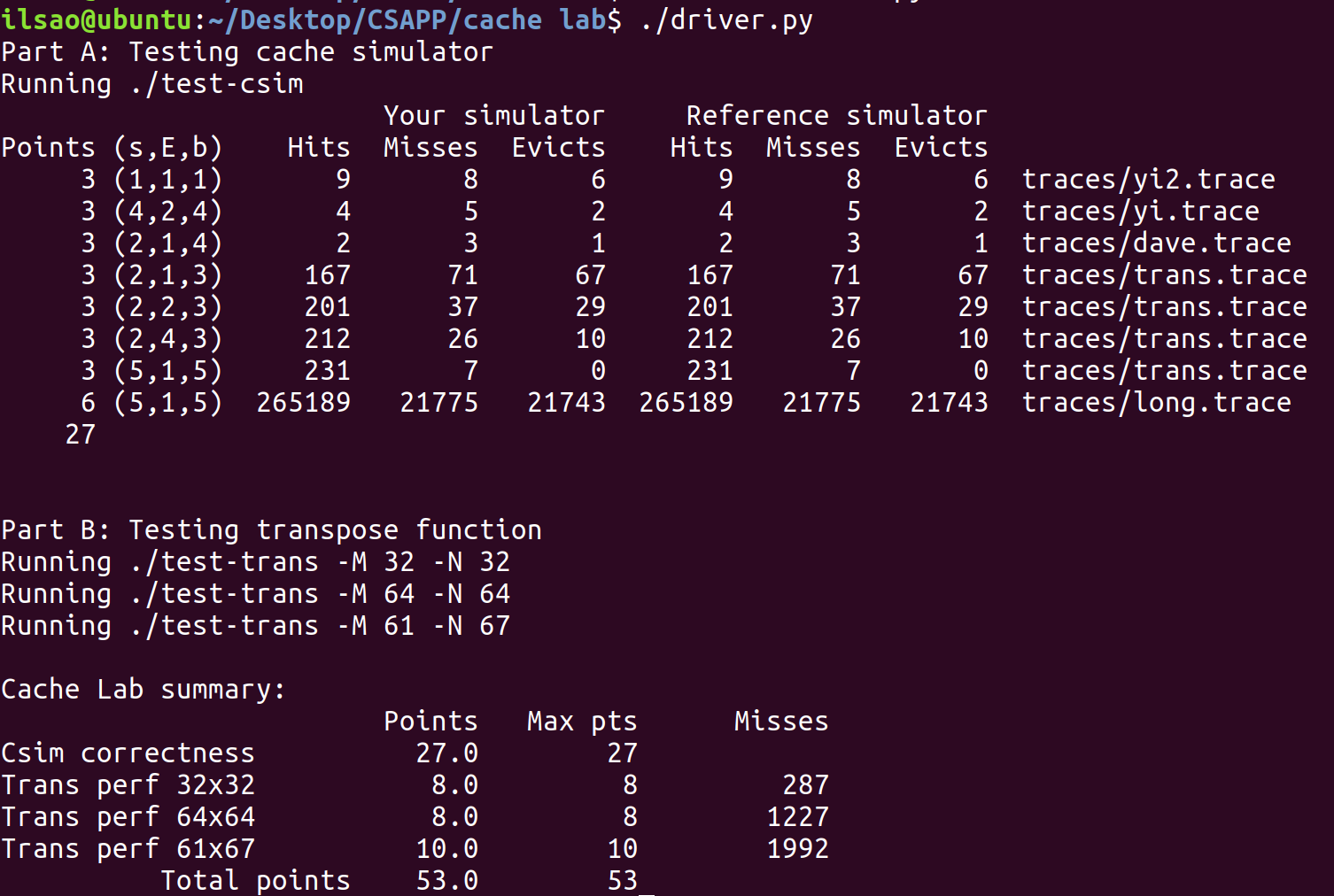
測試
發現可以拿到滿分,喔耶!
以下是完整代碼:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 #include "cachelab.h" #include <stdio.h> #include <stdlib.h> #include <stdbool.h> #include <getopt.h> #include <string.h> #define BUF_SIZE 20 typedef struct _cacheLine { bool valid; unsigned int tag; char *bytes; unsigned int callTime; }cacheLine; typedef struct _cacheSet { cacheLine *line; }cacheSet; typedef struct _dataCache { unsigned int s; unsigned int E; unsigned int b; cacheSet *set ; }dataCache; void ShowHelp () { printf ("Usage: ./csim-ref [-hv] -s <num> -E <num> -b <num> -t <file> \n" ); printf ("Options: \n" ); printf (" -h\t\tPrint this help message.\n" ); printf (" -v\t\tOptional verbose flag.\n" ); printf (" -s <num>\tNumber of set index bits.\n" ); printf (" -E <num>\tNumber of lines per set.\n" ); printf (" -b <num>\tNumber of block offset bits.\n" ); printf (" -t <file>\tTrace file.\n" ); printf ("\n" ); printf ("Examples: \n" ); printf (" linux> ./csim-ref -s 4 -E 1 -b 4 -t traces/yi.trace\n" ); printf (" linux> ./csim-ref -v -s 8 -E 2 -b 4 -t traces/yi.trace\n" ); } void PrintCache (dataCache *cache) { printf ("****** Cache Info ******\n" ); for (int i = 0 ; i < (1 << cache->s); i++) { printf ("set%d: \n" , i); for (int j = 0 ; j < cache->E; j++) printf ("\tline%d: %d %d %s %d\n" , j, cache->set [i].line[j].valid, cache->set [i].line[j].tag, cache->set [i].line[j].bytes, cache->set [i].line[j].callTime); } printf ("************************\n" ); } unsigned int FindTag (dataCache *cache, char *addr) { unsigned int d_addr = strtol(addr, NULL , 16 ); unsigned int tag = d_addr >> ((cache->s) + (cache->b)); return tag; } unsigned int FindSet (dataCache *cache, char *addr) { unsigned int d_addr = strtol(addr, NULL , 16 ); unsigned int mask = (1 << ((cache->s) + (cache->b))) - 1 ; unsigned int set = (d_addr & mask) >> (cache->b); return set ; } unsigned int FindLine (dataCache *cache, unsigned int set , unsigned int tag, unsigned int timer) { unsigned int line = -1 ; for (int i = 0 ; i < cache->E; i++) { if (cache->set [set ].line[i].tag == tag && cache->set [set ].line[i].valid) { line = i; cache->set [set ].line[i].callTime = timer; } } return line; } bool IsSetFull (dataCache *cache, unsigned int set ) { bool flag = true ; for (int i = 0 ; i < cache->E; i++) { if (!cache->set [set ].line[i].valid) flag = false ; } return flag; } void StoreCache (dataCache *cache, unsigned int set , unsigned int tag, unsigned int timer) { for (int i = 0 ; i < cache->E; i++) { if (cache->set [set ].line[i].valid == false ) { cache->set [set ].line[i].valid = true ; cache->set [set ].line[i].tag = tag; cache->set [set ].line[i].callTime = timer; break ; } } } void EvictLine (dataCache *cache, unsigned int set ) { unsigned int minIndex = 0 ; for (int i = 0 ; i < cache->E; i++) minIndex = cache->set [set ].line[i].callTime < cache->set [set ].line[minIndex].callTime ? i : minIndex; cache->set [set ].line[minIndex].valid = false ; } void ShowDetail (char *op, char *addr, char *bytes, char *msg) { printf ("%s %s %s %s" , op, addr, bytes, msg); } bool Simulate (char *tracefile, dataCache *cache, bool v, int *hit_count, int *miss_count, int *evict_count) { FILE *file = fopen(tracefile, "r" ); char buf[BUF_SIZE]; char *op, *addr, *bytes; if (file == NULL ) { printf ("%s: No such file or directory.\n" , tracefile); return false ; } unsigned int timer = 0 ; while (fgets(buf, BUF_SIZE, file) != NULL ) { if (buf[0 ] == 'I' ) continue ;; timer++; op = strtok(buf, " " ); addr = strtok(NULL , "," ); bytes = strtok(NULL , " \n" ); unsigned int set , tag, line; set = FindSet(cache, addr); tag = FindTag(cache, addr); switch (*op) { case 'L' : if ( (line = FindLine(cache, set , tag, timer)) != -1 ) { *hit_count += 1 ; if (v) { ShowDetail(op, addr, bytes, "hit " ); } } else { *miss_count += 1 ; if (!IsSetFull(cache, set )) { StoreCache(cache, set , tag, timer); if (v) { ShowDetail(op, addr, bytes, "miss " ); } } else { *evict_count += 1 ; EvictLine(cache, set ); StoreCache(cache, set , tag, timer); if (v) { ShowDetail(op, addr, bytes, "miss eviction " ); } } } if (v) printf ("\n" ); break ; case 'S' : if ( (line = FindLine(cache, set , tag, timer)) != -1 ) { *hit_count += 1 ; if (v) { ShowDetail(op, addr, bytes, "hit " ); } } else { *miss_count += 1 ; if (!IsSetFull(cache, set )) { StoreCache(cache, set , tag, timer); if (v) { ShowDetail(op, addr, bytes, "miss " ); } } else { *evict_count += 1 ; EvictLine(cache, set ); StoreCache(cache, set , tag, timer); if (v) { ShowDetail(op, addr, bytes, "miss eviction " ); } } } if (v) printf ("\n" ); break ; case 'M' : if ( (line = FindLine(cache, set , tag, timer)) != -1 ) { *hit_count += 1 ; if (v) { ShowDetail(op, addr, bytes, "hit " ); } } else { *miss_count += 1 ; if (!IsSetFull(cache, set )) { StoreCache(cache, set , tag, timer); if (v) { ShowDetail(op, addr, bytes, "miss " ); } } else { *evict_count += 1 ; EvictLine(cache, set ); StoreCache(cache, set , tag, timer); if (v) { ShowDetail(op, addr, bytes, "miss eviction " ); } } } if ( (line = FindLine(cache, set , tag, timer)) != -1 ) { *hit_count += 1 ; if (v) { printf ("hit " ); } } else { *miss_count += 1 ; if (!IsSetFull(cache, set )) { StoreCache(cache, set , tag, timer); if (v) { printf ("miss " ); } } else { *evict_count += 1 ; EvictLine(cache, set ); StoreCache(cache, set , tag, timer); if (v) { printf ("miss eviction " ); } } } if (v) printf ("\n" ); break ; default : break ; } } fclose(file); return true ; } int main (int argc, char *argv[]) { int hit_count = 0 , miss_count = 0 , eviction_count = 0 ; int opt; bool v = false ; int s, E, b; char *tracefile; if (argc == 2 && argv[1 ][1 ] == 'h' ) { ShowHelp(); return 0 ; } if (argc != 10 && argc != 9 ) { printf ("./csim: Missing required command line argument\n" ); ShowHelp(); return -1 ; } while ( (opt = getopt(argc, argv, "hvs:E:b:t:" )) != -1 ) { switch (opt) { case 'h' : ShowHelp(); return 0 ; case 'v' : v = true ; break ; case 's' : s = atoi(optarg); break ; case 'E' : E = atoi(optarg); break ; case 'b' : b = atoi(optarg); break ; case 't' : tracefile = optarg; break ; default : break ; } } unsigned int S = 1 << s; dataCache cache; cache.s = s; cache.E = E; cache.b = b; cache.set = malloc (sizeof (cacheSet) * S); for (int i = 0 ; i < S; i++) { cache.set [i].line = malloc (sizeof (cacheLine) * E); cache.set [i].line->valid = false ; cache.set [i].line->tag = -1 ; cache.set [i].line->callTime = 0 ; } if (!Simulate(tracefile, &cache, v, &hit_count, &miss_count, &eviction_count)) return -1 ; printSummary(hit_count, miss_count, eviction_count); free (cache.set ->line); free (cache.set ); return 0 ; }
Part B 分塊矩陣 在開始此部分之前,讓我們先閱讀官方提供的額外資料 ,文檔中提示該技術可以幫助優化程序。
失策了,文檔裡面的分塊矩陣是大學線性代數裡面的內容。我在看代碼的時候萬分不得其解,結果一查才知道原來是數學還沒學到 :( 。
文檔中提到,分塊矩陣在n較小時性能可能沒有正常優化來的好,但是當n較大時擁有更佳的性能。
分塊矩陣的乘法 下圖是使用分塊矩陣進行乘法運算的代碼。
其中,內層的循環j和k代表分了塊的矩陣做一次乘法運算,而循環i則代表著做完一次乘法後向下進行。
循環jj控制著B分塊矩陣向右進行,而循環kk控制著A分塊矩陣向右進行。
我們需要分辨各變量的遞增順序,最終可以得到矩陣C的運算順序。
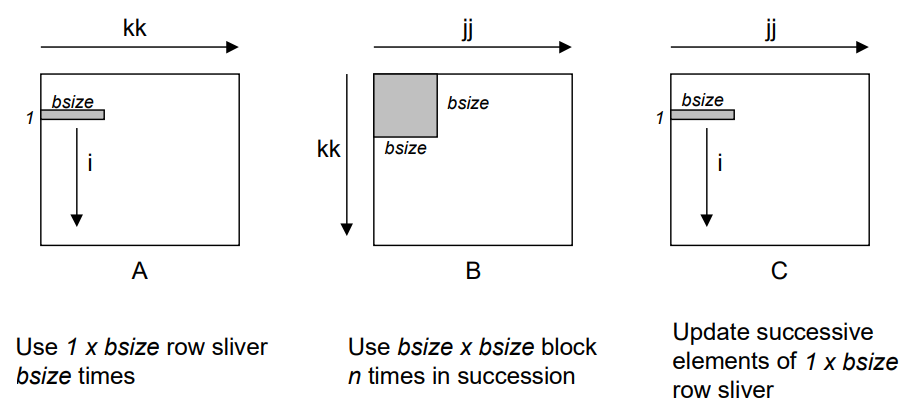
閱讀代碼並搭配以下幾張圖示嘗試理解運算規則。
分塊矩陣的轉置 假設我們有以下矩陣A,從第二列與第三列中間豎著分塊。
則對矩陣A想找到轉置矩陣$A^{T}$,我們有以下方法:
著手優化 $32\times 32$ 我們首先關注於$32 \times 32$大小轉置矩陣運算的優化,並嘗試使用分塊矩陣進行運算。
題目提供了高速緩存的相關信息$(s, E, b)=(5,1,5)$,也就是說,高速緩存中共有32個組,每組只有一條高速緩存行,每個塊可以存儲32個字節(8個int)。綜合所有組,高速緩存最多可以存放1024個字節,也就是矩陣的第0~7行(不產生衝突不命中)。
考慮將bsize設為8(將矩陣劃分為$4 \times 4$的大塊),這樣完整訪問矩陣一次只會有一行$\frac{32}{8}=4$次不命中乘以$32$行$=128$次不命中。
完整一次轉置矩陣運算,AB矩陣應該只會有$128\times 2=256$次不命中。事實上,還需要考慮對角線上的元素會導致衝突不命中,這種情況我們之後再討論。
在以下代碼中,循環i與j代表了大塊的迭代,循環ii和jj代表每個塊中的轉置迭代。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 int i, ii, j, jj, bsize, en, tmp;if (N == 32 ) { bsize = 8 ; en = bsize * (N / bsize); for (i = 0 ; i < en; i += bsize) { for (j = 0 ; j < en; j += bsize) { for (ii = i; ii < i + bsize; ii++) { for (jj = j; jj < j + bsize; jj++) { tmp = A[ii][jj]; B[jj][ii] = tmp; } } } } }
有一個小細節可以注意,我們在設置AB矩陣的值時,通過一個變量tmp作為中轉。
這是書中第五章中提供的優化方法,利用tmp儲存A的元素可以幫助緩解寫/讀相關,並充分利用流水線化處理器的性能。雖然與此實驗沒有太大個關聯,但是不失為一個好的提升性能方法,大家可以注意一下。
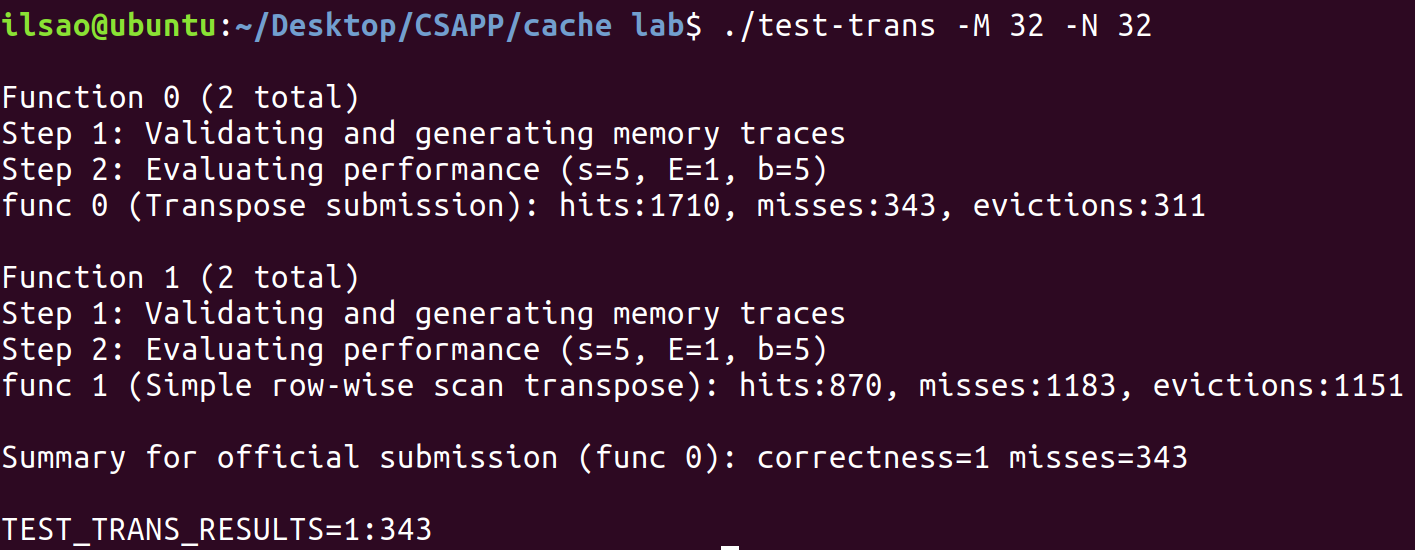
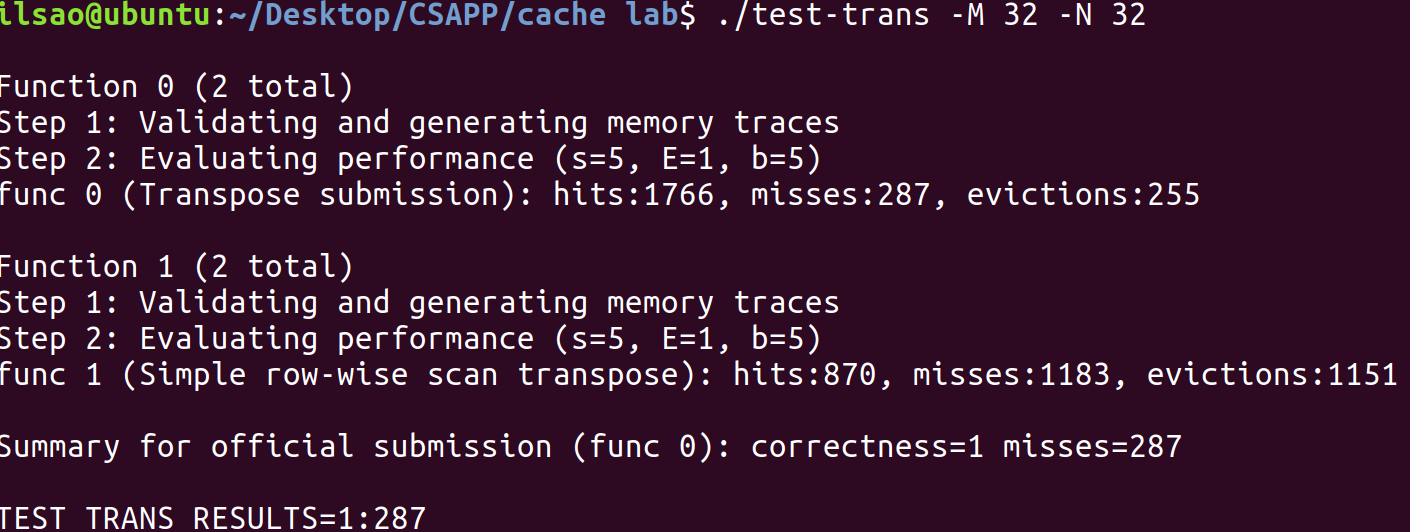
讓我們測試一下:
func 0是我們編寫的函數,可以看到相對於沒有優化過的函數func 1,命中率有極大的提升。
但是我們的不命中數與計算出來的數字有相當大的差距,這是因為對角線元素的衝突不命中導致。
為甚麼A與B矩陣中的對角線元素會造成衝突不命中?回想每個高速緩存最多只能存取一個矩陣的8行,而A與B矩陣的內存地址相鄰。
還要想到對角線的性質,即A[i][j] = A[j][i]。當嘗試將A[ii][jj]寫入B[jj][ii]時,讀取A[ii][jj]不命中,載入高速緩存。寫入B[jj][ii]不命中,嘗試載入高速緩存時,因為B[jj][ii]與A[ii][jj]映射到相同組,而產生衝突不命中。驅逐A矩陣的塊,載入B矩陣的塊。
接下來jj遞增,如果B沒有驅逐A的塊,則A[ii][jj]應該命中,但在此情況下,不命中。剩下情況依此類推。
現在我們想要繼續優化,只需要解決對角線元素的衝突不命中即可。
衝突不命中發生的原因在於,對角線處先訪問A,再訪問B。如果我們可以一次將A的一整行訪問完,然後一次將這些數據寫入B的一整列中,就可以避免衝突不命中的發生。
因為官方文檔限制局部變量最多只能使用12個,我們需要刪除一些之前定義的變量,並使用常數替代。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 int i, ii, j;int a0, a1, a2, a3, a4, a5, a6, a7;if (N == 32 ) { for (i = 0 ; i < 32 ; i += 8 ) { for (j = 0 ; j < 32 ; j += 8 ) { for (ii = i; ii < i + 8 ; ii++) { a0 = A[ii][j+0 ]; a1 = A[ii][j+1 ]; a2 = A[ii][j+2 ]; a3 = A[ii][j+3 ]; a4 = A[ii][j+4 ]; a5 = A[ii][j+5 ]; a6 = A[ii][j+6 ]; a7 = A[ii][j+7 ]; B[j+0 ][ii] = a0; B[j+1 ][ii] = a1; B[j+2 ][ii] = a2; B[j+3 ][ii] = a3; B[j+4 ][ii] = a4; B[j+5 ][ii] = a5; B[j+6 ][ii] = a6; B[j+7 ][ii] = a7; } } } }
這次的測試結果很讚,拿到此部分($32 \times 32$矩陣)滿分。
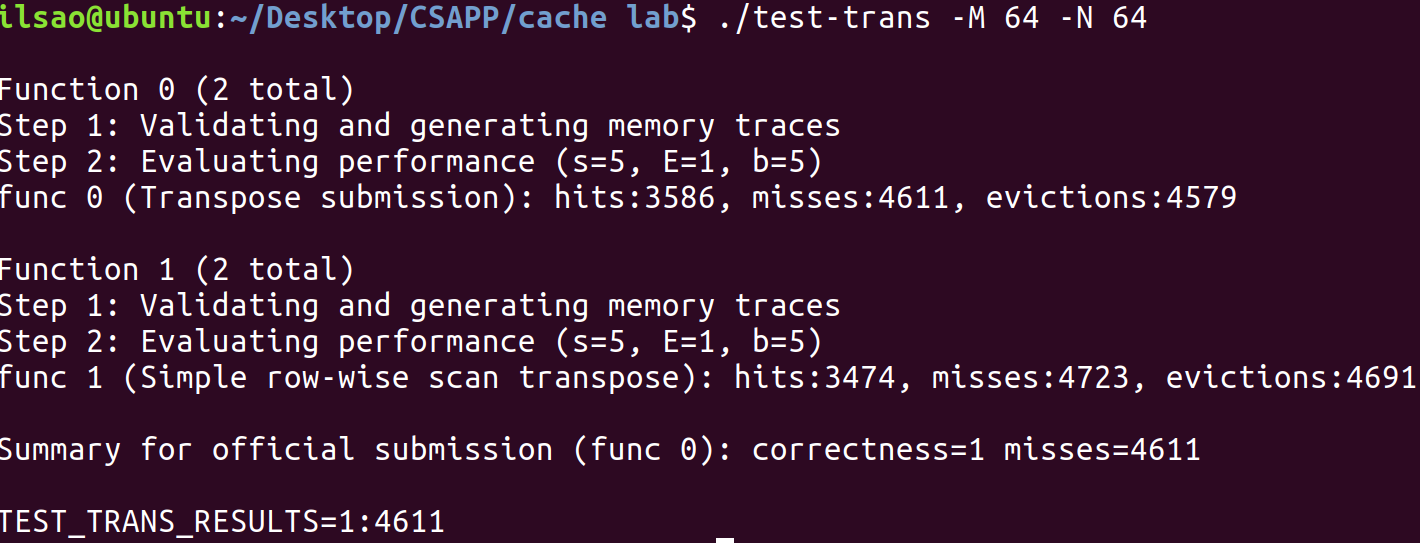
$64 \times 64$ 讓我們嘗試繼續使用分塊矩陣的概念,先套上$32 \times 32$的代碼運行試試看。
竟然有4611個不命中,原本我以為怎麼說起碼也能騙到幾分,沒想到竟然一分都沒有拿到。
讓我們來分析看看為甚麼會發生這種事情。
首先計算高速緩存最多可以存放A矩陣幾行:$\frac{32}{\frac{64}{8}}=4$
我們應該更新策略,使得bsize=4試試看。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 else if (N == 64 ) { for (i = 0 ; i < 64 ; i += 4 ) { for (j = 0 ; j < 64 ; j += 4 ) { for (ii = i; ii < i + 4 ; ii++) { a0 = A[ii][j+0 ]; a1 = A[ii][j+1 ]; a2 = A[ii][j+2 ]; a3 = A[ii][j+3 ]; B[j+0 ][ii] = a0; B[j+1 ][ii] = a1; B[j+2 ][ii] = a2; B[j+3 ][ii] = a3; } } } }
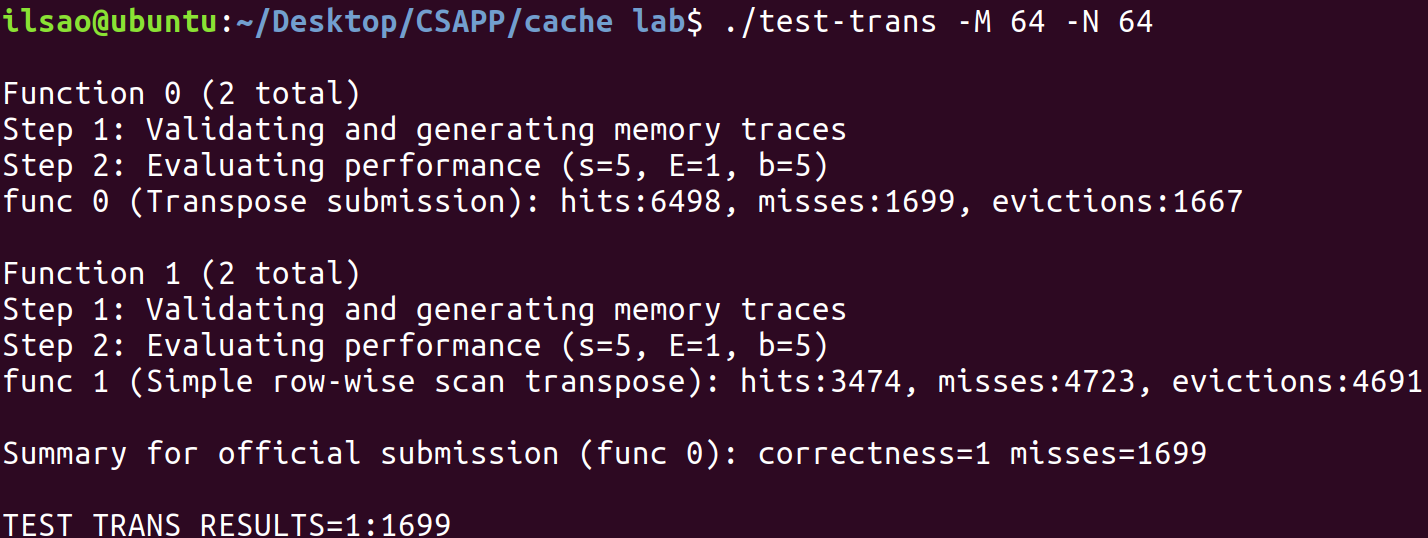
太棒了,不命中數顯著減少,雖然仍舊沒有拿到全部的分數,但是有分了!
其實這樣仍不能完全發揮分塊的優勢,因為最合適的分塊大小應為$4 \times 8$ (高速緩存最多存取4行,每行可以緩存8個int)。
猜想錯誤,我只思考了A矩陣的分塊最佳化,卻忘記了轉置後行列互換的原則,此時B矩陣仍無法發揮分塊的優勢。於是只能將代碼改回。
我們現在來分析一下為甚麼以$4 \times 4$分塊無法取得最佳性能。
當以$4 \times 4$分塊遍歷矩陣A時,效果應和以$4 \times 8$分塊遍歷矩陣A一致。因為矩陣A是以行優先遍歷,所以用$4 \times 4$分塊不會造成更多的不命中。
但若以$4 \times 4$分塊遍歷矩陣B,效果就會大打折扣了。因為當每次高速緩存被填滿(裝填成$4 \times 8$的分塊)時,矩陣B的下次迭代以列優先遍歷而不是行優先遍歷運行,會導致不命中並驅逐存放在高速緩存中還未使用的值。
既然想要盡量減少不命中數,我們考慮將矩陣B的遍歷方式改為行優先。
這裡蠻難想到思路的,我參考了這篇文章 的處理思路。
主要思路是這樣的:將分塊大小保持為$8 \times 8$,並在$8 \times 8$分塊內再次分為4個$4 \times 4$的小分塊。
我們的處理流程是這樣的(稍微修改了參考文章的處理方法,等下會對比兩種方法):
將A矩陣($8 \times 8$分塊內)的左上角($4 \times 4$的小分塊)複製給B矩陣的左上角。
將A矩陣的右上角複製到暫存變量中。
將A矩陣的左下角複製到B矩陣的右上角。
將暫存變量的值複製到B矩陣的左下角。
將A矩陣的右下角複製到B矩陣的右下角。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 else if (N == 64 ) { for (i = 0 ; i < 64 ; i += 8 ) { for (j = 0 ; j < 64 ; j += 8 ) { for (ii = i; ii < i + 4 ; ii++) { a0 = A[ii][j+0 ]; a1 = A[ii][j+1 ]; a2 = A[ii][j+2 ]; a3 = A[ii][j+3 ]; a4 = A[ii][j+4 ]; a5 = A[ii][j+5 ]; a6 = A[ii][j+6 ]; a7 = A[ii][j+7 ]; B[j+0 ][ii] = a0; B[j+1 ][ii] = a1; B[j+2 ][ii] = a2; B[j+3 ][ii] = a3; a0 = A[ii+4 ][j+0 ]; a1 = A[ii+4 ][j+1 ]; a2 = A[ii+4 ][j+2 ]; a3 = A[ii+4 ][j+3 ]; B[j+0 ][ii+4 ] = a0; B[j+1 ][ii+4 ] = a1; B[j+2 ][ii+4 ] = a2; B[j+3 ][ii+4 ] = a3; B[j+4 ][ii] = a4; B[j+5 ][ii] = a5; B[j+6 ][ii] = a6; B[j+7 ][ii] = a7; a0 = A[ii+4 ][j+4 ]; a1 = A[ii+4 ][j+5 ]; a2 = A[ii+4 ][j+6 ]; a3 = A[ii+4 ][j+7 ]; B[j+4 ][ii+4 ] = a0; B[j+5 ][ii+4 ] = a1; B[j+6 ][ii+4 ] = a2; B[j+7 ][ii+4 ] = a3; } } } }
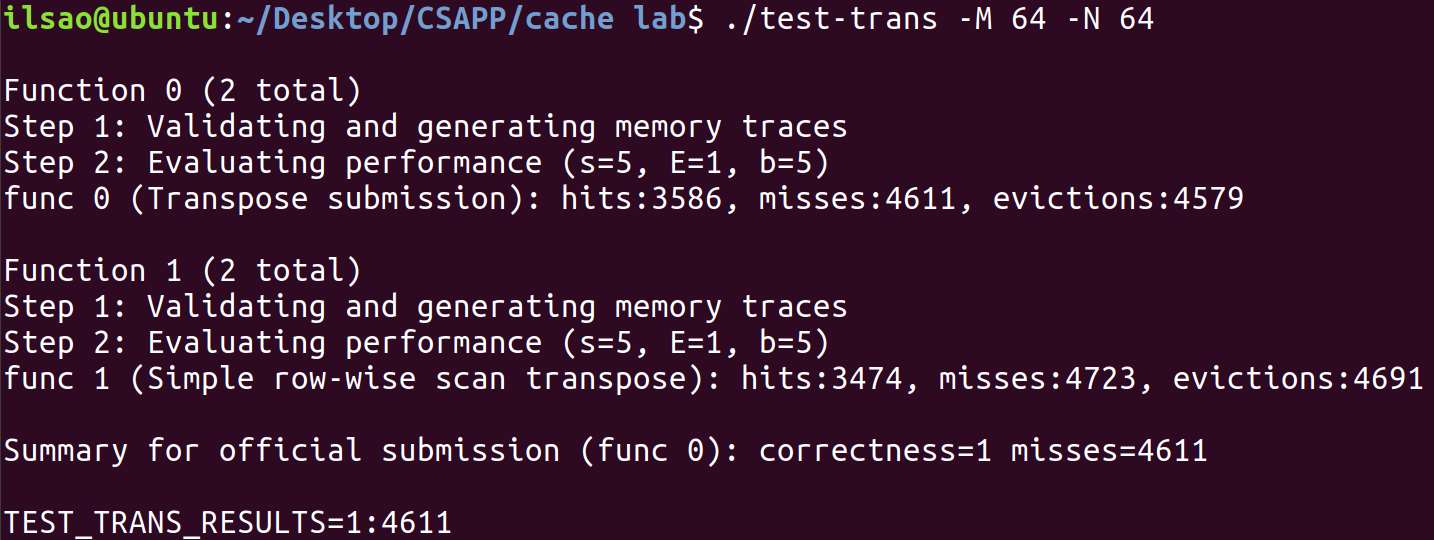
壞了,測試完發現不命中數不減反增,不命中數增加到2659。分析看看哪裡想錯了。
問題出在矩陣A左下塊將數據複製到矩陣B右上塊時,因為變量a4~a7被用於儲存矩陣A右上塊的值,所以在讀取矩陣A左下塊數據時無法一次將矩陣A右下塊一起讀取。
讓我們嘗試復刻文章中原本的方法(疑問,why this work? ):
將矩陣A左上和右上一次性複製到矩陣B。
將矩陣B的數據暫存到暫存變量中。
將矩陣A的左下複製到矩陣B的右上。
將暫存變量中的數據複製到矩陣B的左下。
把矩陣A的右下複製到矩陣B的右下。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 else if (N == 64 ) { for (i = 0 ; i < 64 ; i += 8 ) { for (j = 0 ; j < 64 ; j += 8 ) { for (ii = i; ii < i + 4 ; ii++) { a0 = A[ii][j+0 ]; a1 = A[ii][j+1 ]; a2 = A[ii][j+2 ]; a3 = A[ii][j+3 ]; a4 = A[ii][j+4 ]; a5 = A[ii][j+5 ]; a6 = A[ii][j+6 ]; a7 = A[ii][j+7 ]; B[j+0 ][ii] = a0; B[j+1 ][ii] = a1; B[j+2 ][ii] = a2; B[j+3 ][ii] = a3; B[j+0 ][ii+4 ] = a4; B[j+1 ][ii+4 ] = a5; B[j+2 ][ii+4 ] = a6; B[j+3 ][ii+4 ] = a7; } for (jj = j; jj < j + 4 ; jj++) { a0 = B[jj][i+4 ]; a1 = B[jj][i+5 ]; a2 = B[jj][i+6 ]; a3 = B[jj][i+7 ]; a4 = A[i+4 ][jj]; a5 = A[i+5 ][jj]; a6 = A[i+6 ][jj]; a7 = A[i+7 ][jj]; B[jj][i+4 ] = a4; B[jj][i+5 ] = a5; B[jj][i+6 ] = a6; B[jj][i+7 ] = a7; B[jj+4 ][i+0 ] = a0; B[jj+4 ][i+1 ] = a1; B[jj+4 ][i+2 ] = a2; B[jj+4 ][i+3 ] = a3; } for (ii = i; ii < i + 4 ; ii++) { a0 = A[ii+4 ][j+4 ]; a1 = A[ii+4 ][j+5 ]; a2 = A[ii+4 ][j+6 ]; a3 = A[ii+4 ][j+7 ]; B[j+4 ][ii+4 ] = a0; B[j+5 ][ii+4 ] = a1; B[j+6 ][ii+4 ] = a2; B[j+7 ][ii+4 ] = a3; } } } }
可以發現不命中數減少到1227。
$61 \times 67$ 測試不同分塊大小即可,這邊選擇$16 \times 16$大小的分塊。
1 2 3 4 5 6 7 8 9 10 11 else if (N == 67 ) { for (i = 0 ; i < 67 ; i += 16 ) { for (j = 0 ; j < 61 ; j += 16 ) { for (ii = i; ii < i+16 && ii < 67 ; ii++) { for (jj = j; jj < j+16 && jj < 61 ; jj++) { B[jj][ii] = A[ii][jj]; } } } } }
不命中數為1992,通過。
評分 如果是python3無法直接運行提供的driver.py。
我們先把官方提供的driver.py刪除,然後下載網上別人提供的python3版本,並提供可執行權限:
1 2 wget https://gitee.com/lin-xi-269/csapplab/raw/master/lab5cachelab/cachelab-handout/driver.py chmod +x driver.py
然後就可以執行評分了:
後記 這個lab寫起來特別累,是至今為止寫起來最無助的一個lab。
Part A讓我充分明白自己實際動手寫代碼的能力過於薄弱。我在自己實現完模擬器後去網上搜了一下別人寫的代碼,發現竟然有人可以用一百多行代碼就把模擬器實現出來,大為震驚。
Part B更是讓我體會到了大佬和我的差距,單做Part B就花了我兩天的時間。做$32 \times 32$時還稍微可以接受,就是在第一次閱讀web aside時無法理解分塊矩陣乘法的代碼。特別花了一個小時搜索了線性代數相關的章節拿來看,再盯著好幾層for循環人肉模擬CPU才堪堪弄懂。話說$32 \times 32$好歹我自己實現並拿到了滿分,但到$64 \times 64$這邊就徹底沒招了。這部分如果不參考大佬的文章,我最終優化只能到1699個不命中,連一半的分數都沒拿到。雖然搞懂了大佬的思路,但是具體代碼實現為何這樣寫,以及為何我修改的代碼與大佬的代碼差距會如此巨大也不是特別清楚。如果各位師傅有人能賜教,本人不勝感激。
CSAPP硬件篇到此為止,接下來是令人激動的軟件篇!


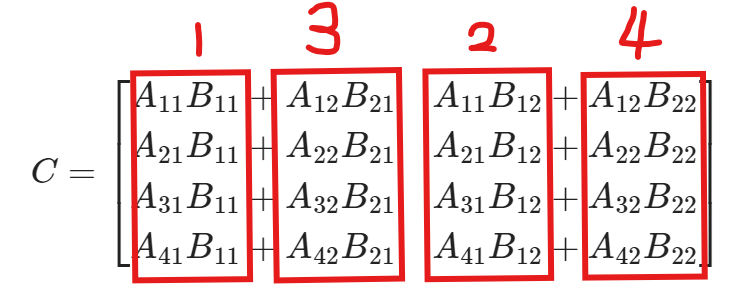








![[GAMES 101] Rasterization 筆記](/pictures/SAO.jpg)


