優化編譯器的能力和侷限性

編譯器只能對程序使用安全的優化。例如以下代碼：

1
2
3
4
5
6
7
8
void twiddle1(long *xp, long *yp) {
	*xp += *yp;![[A Way Out.url]]
	*xp += *yp;
}

void twiddle2(long *xp, long *yp) {
	*xp += 2 * (*yp);
}

以上兩函數看起來實現的功能相似。的確，當*xp與*yp指向兩個不同的內存地址時兩個函數的行為相同。但如果兩個指針指向相同的內存地址，則twiddle1()會把值翻4倍，而twiddle2()只會把值翻3倍。

這種兩個指針可能指向同一個內存位置的情況稱內存別名使用(memory aliasing)，會嚴重限制編譯器優化代碼性能。

還有一個妨礙優化的因素是函數調用，考慮以下代碼：

1
2
3
4
5
6
7
8
9
long f();

long func1() {
	return f() + f();
}

long func2() {
	return 2 * f();
}

直覺上可能會認為以上兩函數具有相同的行為，但是如果f()的結果跟隨其執行次數上升而有不同的執行結果時，二函數的返回值則會有所不同。

練習題

5.1

*xp與*yp的值都為0。

5.2

數學問題，此略。

表示程序性能

我們使用每元素的周期數(Cycles Per Element, CPE) 表示程序性能。

程序示例

我們定義一個向量數據結構：

1
2
3
4
typedef struct {
	long len;
	data_t *data;
}vec_rec, *vec_ptr;

其中，data_t是我們自行使用typedef定義出來的數據類型。

接著，我們定義一個函數，它的作用是對向量做一系列操作。之後都會針對這個函數進行一系列優化。

1
2
3
4
5
6
7
8
9
void combine1(vec_ptr v, data_t *dest) {
	long i;
	*dest = IDENT;
	for(i = 0; i < vec_length(v); i++) {
		data_t val;
		get_vec_element(v, i, &val);
		*dest = *dest OP val;
	}
}

對以上代碼在具有Intel Core i7 Haswell的參考機上測試，得到以下結果(單位為CPE)。

1

消除循環的低效率

在combine1()中，我們調用函數vec_length()作為for循環的邊界條件。由於向量的長度不會在此函數運行期間改變，所以每次循環都調用函數取得向量長度屬於浪費，我們將取得向量長度的代碼移動到循環外。

1
2
3
4
5
6
7
8
9
10
void combine2(vec_ptr v, data_t *dest) {
	long i;
	long length = vec_length(v);
	*dest = IDENT;
	for(i = 0; i < length; i++) {
		data_t val;
		get_vec_element(v, i, &val);
		*dest = *dest OP val;
	}
}

2

可以看到性能有了略微提升。我們稱這種優化代碼移動(code motion)

減少過程調用

combine2的代碼給次循環都調用get_vec_element()獲取元素，非常低效。我們新設計一個函數get_vec_start()作為替代，然後使用數組形式訪問數據。

1
2
3
4
5
6
7
8
9
void combine3(vec_ptr v, data_t *dest) {
	long i;
	long length = vec_length(v);
	data_t *data = get_vec_start(v);
	*dest = IDENT;
	for(i = 0; i < length; i++) {
		*dest = *dest OP data[i];
	}
}

3

可惜，這次改動反而讓性能變得更差。循環中的其他操作造成瓶頸，限制性能超過調用get_vec_element()。

消除不必要的內存引用

在combine3中，每次循環都需要從內存中讀取*dest的值。為了消除這種不必要的內存引用，我們引入一個臨時變量acc：

1
2
3
4
5
6
7
8
9
10
void combine4(vec_ptr v, data_t *dest) {
	long i;
	long length = vec_length(v);
	data_t *data = get_vec_start(v);
	data_t acc = IDENT;
	for(i = 0; i < length; i++) {
		acc = acc OP data[i];
	}
	*dest = acc;
}

4

這次程序性能有了顯著提升。

練習題

5.4

A. %xmm0在-O2中當累積者，在-O1中當臨時變量。

B. 是的。

C. 因為每次循環開頭讀取的值與循環末尾寫入的值相同，所以可以這樣變化。

理解現代處理器

有兩種下界限制了程序的最大性能：

  1. 延遲界線(latnecy bound)：數據相關導致下一條代碼執行前，當前代碼必須先執行完。
  2. 吞吐量界線(throughput bound)：處理器功能單元的原始計算能力。

整體操作

5

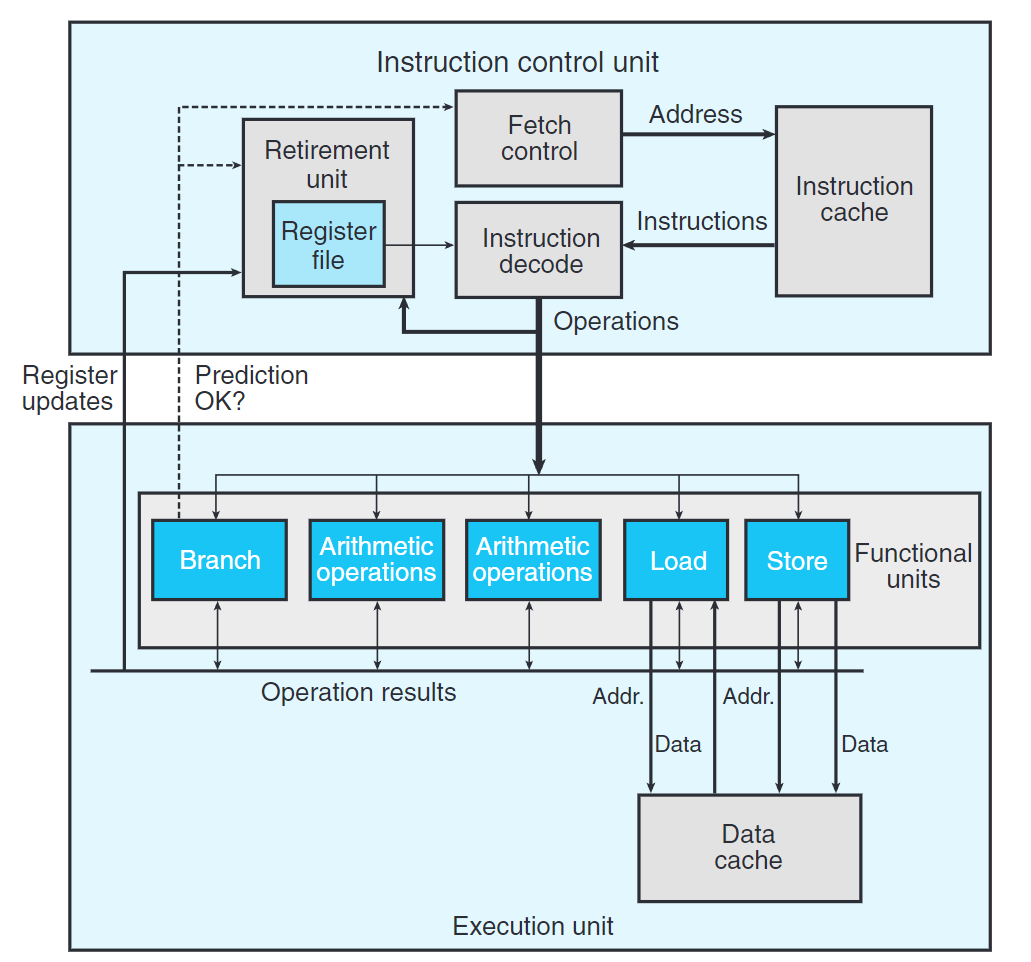
上圖示現代微處理器的簡化版示意圖。這種處理器稱為超標量(superscalar)，可以在一個時鐘周期內執行多個操作，而且是亂序(out-of-order) 的。

整個設計分為兩個部分：

  1. 指令控制單元(Instruction Control Unit, ICU)：從內存讀出指令序列，據此生成針對程序數據的基本操作。
  2. 執行單元(Execution Unit, EU)：執行ICU生成的操作。

ICU從指令高速緩存(instruction cache) 中讀取指令。通常ICU會在當前執行指令的很早之前取指，這樣它才有時間對指令譯碼並發送到EU。

當程序遇到分支，ICU使用一種稱為分支預測(branch prediction) 的技術。通過投機執行(speculative execution) ，處理器會在確定分支正確性前開始執行這些指令。如果之後發現預測錯誤，會將狀態重新設置道分支點的狀態，並取出正確的指令。標記為Fetch Control的塊包括分支預測，以確定取出那些指令。

Insturction Decode 接收程序指令，並將它們轉換成一組基本操作(或稱微操作)。

1
addq %rax, %rdx

以上代碼在典型x86實現中，會被轉化成一個操作。

1
addq %rax, 8(%rdx)

以上代碼則會被轉換成三個操作，一個讀內存值，一個將%rax與內存值相加，一個寫內存值。

EU接收來自取指單元的操作。這些操作被分派到功能單元(Functional Units) 中並執行實際操作。

讀寫內存由加載和存儲單元實現，通過數據高速緩存(data cache) 來訪問內存。

使用投機執行技術對操作求值，但結果暫時不會存放回寄存器或內存中。當分支操作送到EU，確定分支預測正確性後，若錯誤則丟棄計算結果，否則將數據寫回存儲器。

算術運算(Arithmetic operations) 塊通常不只一個，使得操作可以並行運行。

ICU中的退役單元(retirement unit) 控制著指令的結束。譯碼時，指令被放在對列中，直到分支預測正確而退役，或分支預測錯誤而被清空(flushed)，此時丟棄計算出來的結果。

控制操作數在執行單元間傳送的機制稱為寄存器重命名(register renaming)。

功能單元的性能

延遲(latency)：完成運算所需的總時間。

發射時間(issue time)：兩個同類型指令連續執行之間所需的最短周期數。

容量(capacity)：能執行該計算的功能單元數量。

完全流水線化(fully pipelined)：發射時間為1者。

吞吐量：發射時間的倒數。

練習題

5.5

A. $2n$次加法(答案說$n$次，我猜他省略了整數加法i++)，$2n$次乘法

B. 循環中消耗最大的是a[i] * xpwr和x * xpwr，而這兩個乘法可以並行，占五個時鐘週期。而result和x沒有依賴關係，可以將加法放到下次迭代計算，所以CPE為5。

5.6

A. $n$次加法，$n$次乘法。

B. 此函數中result和x有先後依賴關係，不可將本次迭代的計算延遲到下次迭代計算。所以CPE為$5+3=8$。

C. 5.5沒有數據冒險。

循環展開

循環展開通過增加每次迭代計算元素的數量，減少循環迭代的次數。

循環展開從兩方面增進程序的性能：

  1. 減少不直接參與結果計算的操作數量，例如循環索引計算或條件分支。
  2. 循環展開提供一些方法進一步變化代碼，減少計算中關鍵路徑上的操作數量。

若將一個循環按任意因子$k$展開，稱$k\times 1$循環展開。

我們令向量長度為$n$，則此循環的上限應為$n-k+1$，且循環內對元素$i$到$i+k-1$應合併運算。每次迭代索引$i$加$k$。

由於最大循環索引$i+k-1$會小於$n$，所以我們需要第二個循環，每次循環處理一個元素直到最後。此循環會執行$0\sim k-1$次。

6

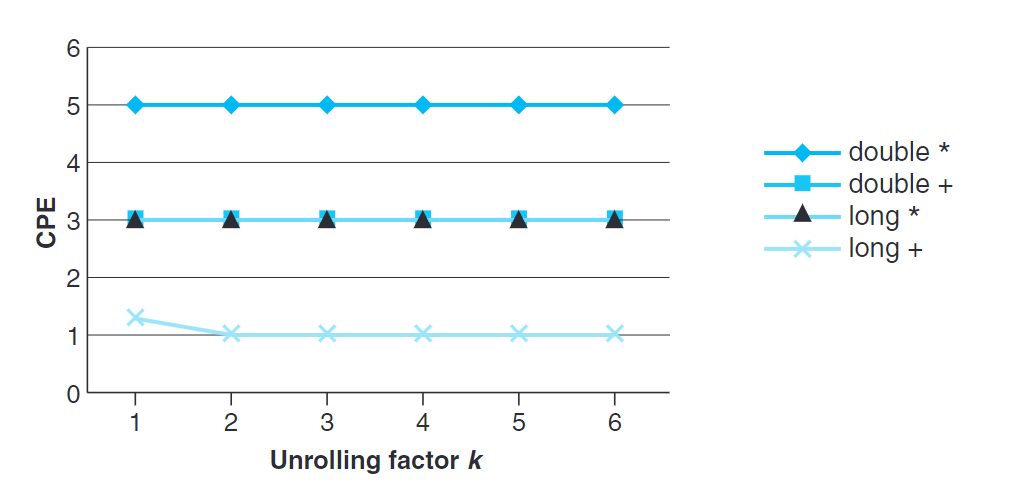
觀察上圖我們可以發現，這種變換只改進了整數加法的性能。

7

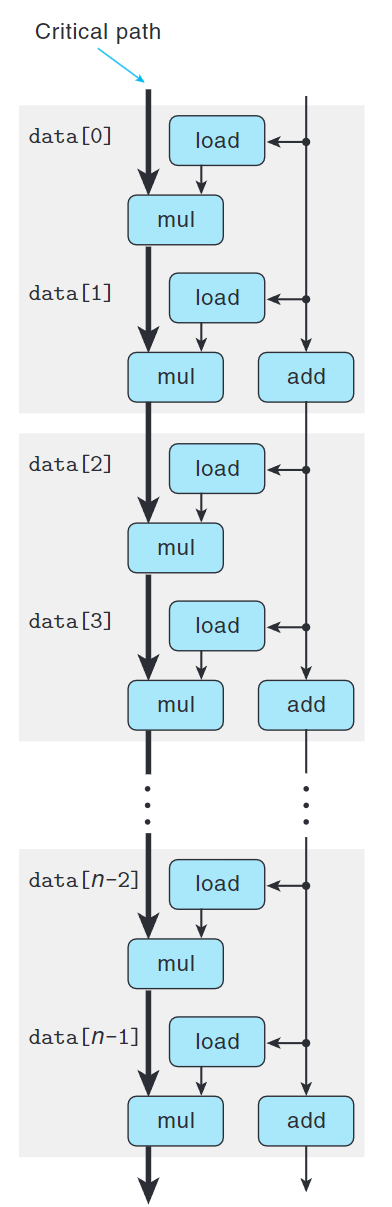
假設操作為double的乘法，每次操作需要從內存中加載一個數組元素並將這個值乘以累積值。

通過上圖我們可以觀察出，雖然關鍵路徑上迭代的次數減半，但是每次迭代中仍有兩個順序的乘法操作，這就是限制性寧提升的關鍵。

練習題

5.7

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void combine5(vec_ptr v, data_t *dest) {
	long i;
	long length = vec_length(v);
	long limit = length - 4;
	data_t *data = get_vec_start(v);
	data_t acc = IDENT;

	/* Combine 5 element at a time */
	for (i = 0; i < limit; i += 5) {
		acc = (acc OP data[i]) OP data[i + 1];
		acc = (acc OP data[i + 2]) OP data[i + 3];
		acc = acc OP data[i + 4];
	}

	/* Finish any remaining elements */
	for (; i < length; i++) {
		acc = acc OP data[i];
	}
	*dest = acc;
}

提高並行性

由於我們將累積值放在單個變量中，在前面的計算完成前，都不能計算acc的新值，導致性能被限制。

多個累積變量

通過將偶數元素積累在acc0中，將奇數元素累積在acc1中，我們可以實現$2\times 2$循環展開。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void combine6(vec_ptr v, data_t *dest) {
	long i;
	long length = vec_length(v);
	long limit = length - 1;
	data_t *data = get_vec_start(v);
	data_t acc0 = IDENT;
	data_t acc1 = IDENT;

	/* Combine 2 element at a time */
	for (i = 0; i < limit; i += 2) {
		acc0 = acc0 OP data[i];
		acc1 = acc1 OP data[i+1];
	}

	/* Finish any remaining elements */
	for (; i < length; i++) {
		acc0 = acc0 OP data[i];
	}
	*dest = acc0 OP acc1;
}

8

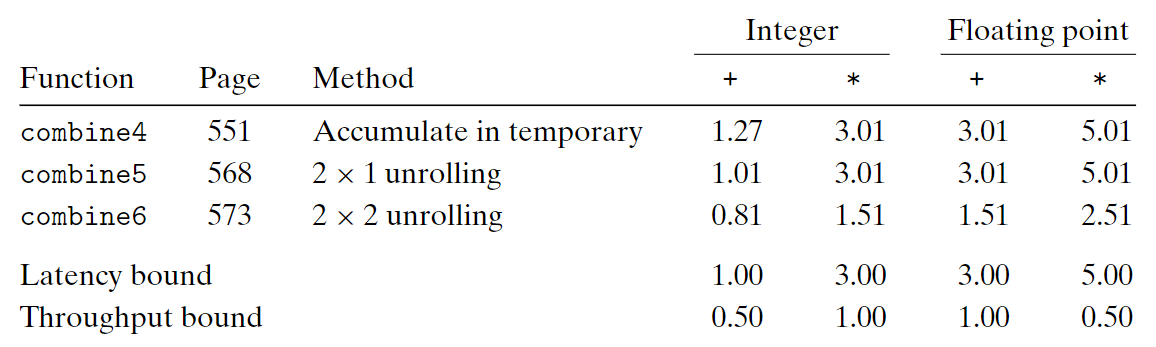
上表可知我們打破了延遲界線，代表我們不需要延遲一個加法或乘法以等待上一個操作完成。

9

10

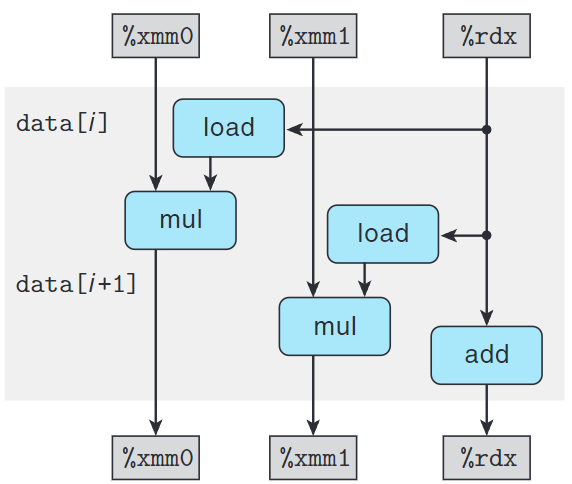
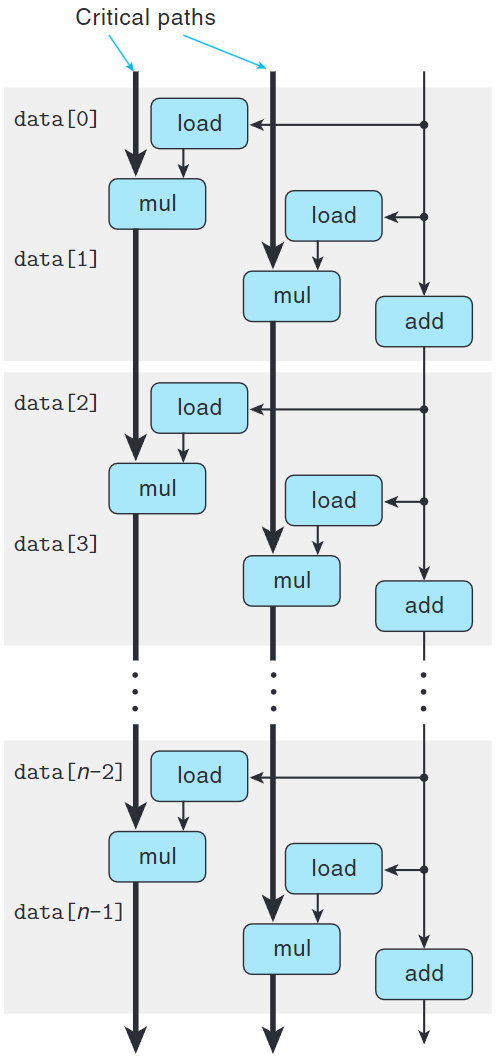
可以看到關鍵路徑上的操作減半，所以對比combine5和combine6可以發現CPE幾乎砍半。

我們可以通過將循環展開$k$次，並行$k$次得到$k \times k$循環展開。

通常，只有所有執行該操作的功能單元的流水線都是滿的時，程序才能達到吞吐量界線。

對延遲$L$，容量$C$的操作而言，要求循環展開因子$k \geq C \cdot L$。

例如，浮點乘有$C=2, \ L=5$，則循環因子為$k \geq 10$。

重新結合變換

考慮將combine5中的：

1
acc = (acc OP data[i]) OP data[i+1];

括號修改順序形成新函數combine7：

1
acc = acc OP (data[i] OP data[i+1]);

這種行為我們稱為重新結合變換(reassociation transformation)。

因為括號改變元素與累積值acc的合併順序，我們稱$2\times 1a$循環展開。

11

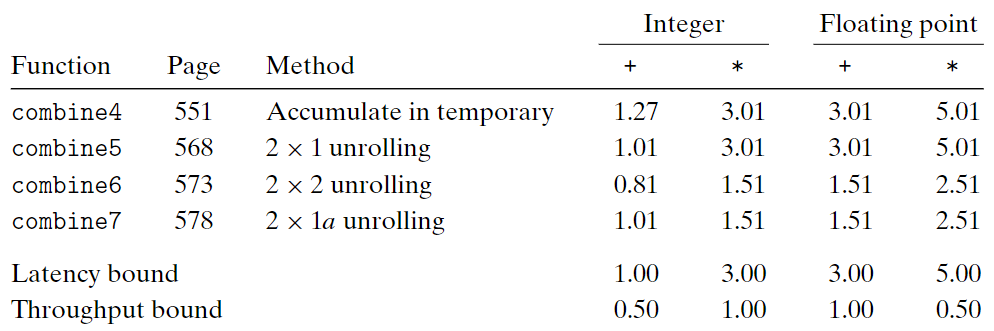
之所以會有這樣的提升是因為後者解除了數據依賴。

練習題

5.8 CPE = 5P/3

A1: 5.00

A2: 3.33

A3: 1.67

A4: 1.67

A5: 3.33

一些限制因素

寄存器溢出

如果我們的並行度$p$超過可用的寄存器數量，那麼編譯器會訴諸溢出(spilling)，將某些臨時值存放在內存中，通常在運行時堆棧上分配空間。

一旦編譯器必須訴諸溢出，那維護多個寄存器的優勢就可能會消失，使CPE上升。

分支預測和預測錯誤處罰

因為條件傳送指令可以被實現為普通指令流水線化處理，沒必要猜測條件是否滿足，所以沒有猜測錯誤處罰。

因為條件傳送指令不會改變PC，且現代處理器可以亂序執行，所以流水線可以先運行其他指令，等條件傳送指令計算完再執行該指令。

現在我們關心如何保證分支預測處罰不會阻礙程序效率？

  1. 不用過分關心可預測的分支：例如可預測的邊界檢查
  2. 書寫適合用條件傳送實現的代碼
    之前說過條件傳送指令不會因預測錯誤而受處罰。所以如果可以，我們想要用條件重送指令替代分支。即，使用功能式指令替代命令式指令。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void minmax1(long a[], long b[], long n) {
	long i;
	for (i = 0; i < n; i++) {
		if (a[i] > b[i]) {
			long t = a[i];
			a[i] = b[i];
			b[i] = t;
		}
	}
}

void minmax2(long a[], long b[], long n) {
	long i;
	for (i = 0; i < n; i++) {
		long min = a[i] < b[i] ? a[i] : b[i];
		long max = a[i] > b[i] ? a[i] : b[i];
		a[i] = min;
		b[i] = max;
	}
}

以上代碼minmax2()更容易被編譯成條件傳送指令。

練習題

5.9

1
2
long min = src1[i1] < src2[i2] ? src1[i1++] : src2[i2++];
dest[id++] = min;

理解內存性能

加載的性能

我們可以簡單編寫一系列互相依賴的加載操作來計算加載性能：

1
2
3
4
5
6
7
8
long list_len(list_ptr ls) {
	long len = 0;
	while(ls) {
		len++;
		ls = ls -> next;
	}
	return len;
}
1
2
3
4
5
.L3:
	addq $1, %rax
	movq (%rdi), %rdi
	testq %rdi, %rdi
	jne .L3

可以觀察出movq是循環中的性能瓶頸。後面的%rdi值都依賴於這個操作。在參考機上我們測得CPE為4.0，與參考機中L1級cache的4週期訪問時間一致。

存儲的性能

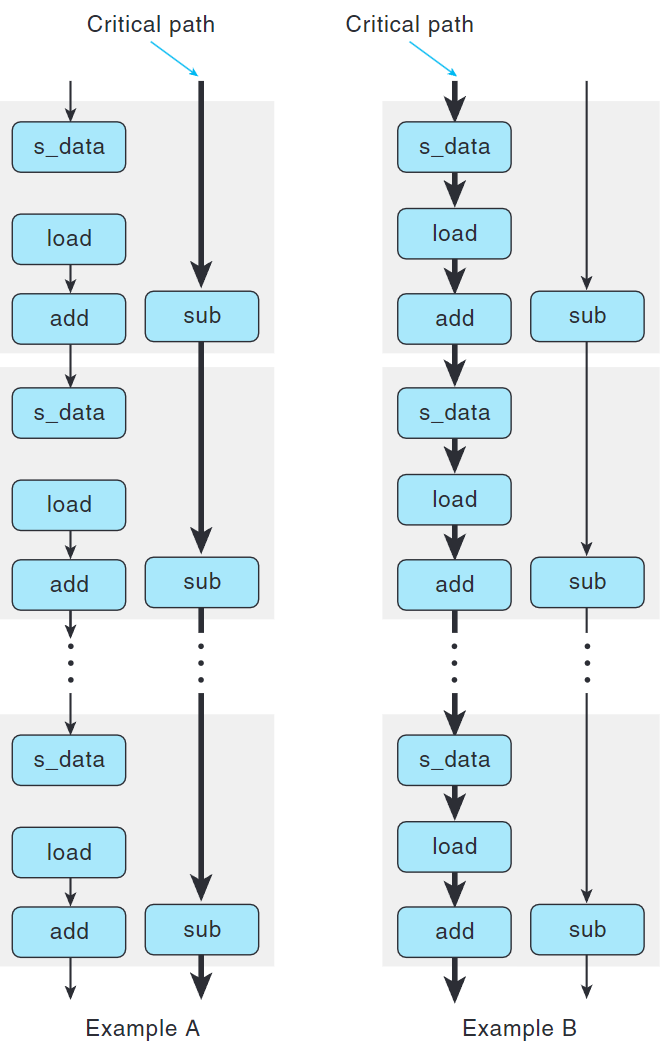
存儲操作不影響任何寄存器值，除非有加載操作否則不會產生數據相關。

12

由於Example A沒有產生寫/讀相關(write/read dependency) 所以CPE較小，CPE=1.3。

而Example B產生寫/讀相關所以CPE較大，CPE=7.3。

13

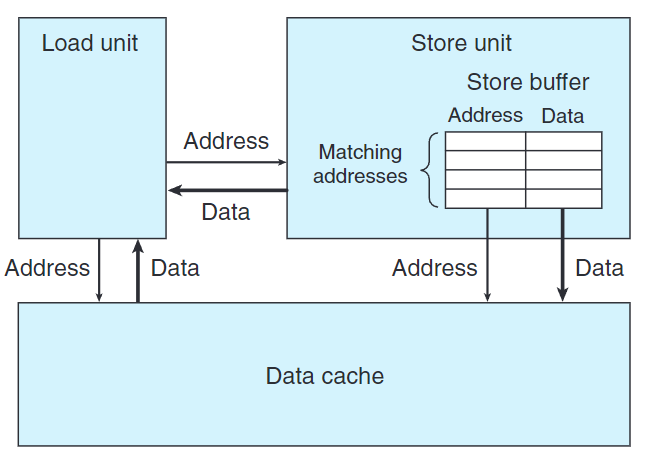
上圖是加載和存儲執行單元。

存儲單元包含一個存儲緩衝區(store buffer)，它包含已經被發射到存儲單元但還沒完成(包括更新數據高速緩存)存儲操作的地址和數據。

write_read()內循環匯編碼如下：

1
2
3
4
5
6
7
# src in %rdi, dst in %rsi, val in %rax
.L3:
	movq %rax, (%rsi)
	movq (%rdi), %rax
	addq $1, %rax
	subq $1, %rdx
	jne .L3

其中，movq %rax, (%rsi)被拆分成兩步：s_addr計算地址，並在存儲緩衝區創建該條地址目的條目。s_data設置該條目的數據。

14

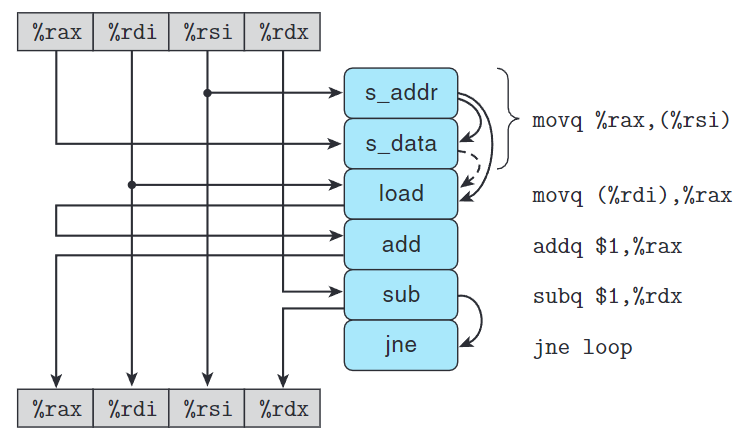
s_data和load有數據相關，但是有條件：如果地址相同，load必須等s_data將數據放入緩衝區。如果地址不同，兩個操作可以獨立運行。

15

練習題

5.10

A. a全項左移

B. a全項被設為a[0]

C. B沒有寫/讀相關

D. CPE=1.2，因為沒有寫/讀相關，所以與A同

5.11

此次寫入的p[i]在i自增後，與下次的p[i-1]代表同一地址。產生寫/讀相關。

5.12

1
2
3
4
5
6
7
8
void psum(float a[], float p[], long n) {
	long i;
	p[0] = a[0];
	float tmp = a[0];
	for (i = 1; i< n; i++)
		tmp += a[i];
		p[i] = tmp;
}

確認和消除性能瓶頸

Unix系統提供一個程序剖析(profiling) 的工具GPROF。

我們需要為需要剖析的程序添加標誌-Og和-pg：

1
gcc -Og -pg prog.c -o prog

然後正常執行：

1
./prog

它會產生一個文件gmon.out，且通常會運行的比正常慢2倍。

調用GPROF來分析gmon.out中的數據：

1
gprof prog

需要注意，對於運行時間少於1秒的程序GPROF的計時不準確。